CHAPITRE_2: LA VALEUR TEMPS DE L’ARGENT ET LES TAUX D’INTERET

PLAN DU COURS

 

 

-INTRODUCTION

- CONCEPTS FONDAMENTAUX : Taux d’intérêt nominal et réel, Taux d’intérêt proportionnel, inflation et taux d’intérêt, taux d’intérêt simple et taux d’intérêt composé.

• VALEUR ACTUELLE ET VALEUR FUTURE.
• ANNUITES 
• EMPRUNTS INDIVIS.
• RENTES PERPETUELLES
• CONCLUSION

--------------

INTRODUCTION

Les mouvements d’entrées et de sorties des flux monétaires d’une opération réalisée par une entreprise et un partenaire s’effectuent généralement à différents moments. Une même somme d’argent exprimée à deux dates différentes du temps, n’a pas la même valeur. La valeur temps de l'argent (VTA) est un concept fondamental en finance, affirmant qu'un montant d'argent aujourd'hui vaut plus que la même somme à l'avenir en raison de son potentiel de gain. Ce principe est intimement lié aux taux d'intérêt, qui déterminent le coût de l'emprunt et le rendement des investissements. Les effets de la composition des intérêts jouent un rôle crucial, car des intérêts composés permettent de générer des gains exponentiels sur le capital investi, amplifiant ainsi la valeur future de l'argent.

Cependant, l'inflation représente un défi pour la VTA, car elle réduit le pouvoir d'achat de l'argent au fil du temps. Une inflation élevée peut éroder les rendements des investissements, rendant essentiel le calcul de la valeur réelle des flux de trésorerie futurs.

Les annuités facilitent la gestion de la dette en structurant le remboursement d'un emprunt en paiements réguliers, tandis que les emprunts indivis, où plusieurs emprunteurs partagent les responsabilités d'un même prêt, ajoutent une dimension de collaboration financière.

De plus, la notion de perpétuité, illustrée par la formule de Gordon-Shapiro, permet d'évaluer la valeur actuelle des flux de trésorerie futurs qui se prolongent indéfiniment.

 

 

 ----- 

 

I-                     LES CONCEPTS FONDAMENTAUX

 

1-    Les flux

 

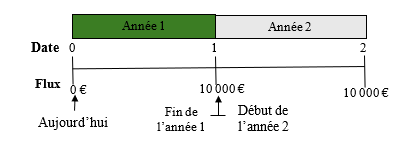
La Finance, décrit des opérations qui se traduisent par des flux financiers : des encaissements ou des décaissements pour ne parler que des plus évidents. Il est possible de représenter graphiquement une séquence de flux à l’aide d’un échéancier des flux ou diagramme des flux (timeline). La construction d’un échéancier est souvent la première étape dans la compréhension et la résolution de problèmes financiers. Pour illustrer cela, prenons le cas d’une banque s’apprêtant à recevoir d’un emprunteur deux paiements égaux de 10 000 € à la fin des deux prochaines années. Ces informations sont représentées sur l’échéancier suivant :

 

 

              

                              

                     

                                            

La date 0 est par convention la date d’aujourd’hui. La date 1 représente la fin de la première période. L’espace entre la date 0 et la date 1 représente le temps qui s’écoule entre ces deux dates – ici, la première année du prêt. À noter que la date 1 est à la fois la fin de l’année 1 et le début de l’année 2.

Dans cet exemple, les flux reçus par la banque sont positifs. Dans la plupart des cas, une opération financière implique des flux positifs (inflows) et négatifs (outflows). Lorsqu’une banque prête 10 000 € à un de ses clients qui remboursera en deux versements de 6 000 € à la fin des deux prochaines années, l’échéancier est, du point de vue de la banque :

 

 

          

        

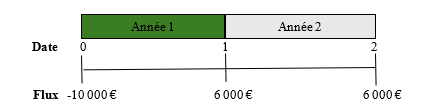
Le premier flux est précédé du signe moins puisqu’il s’agit d’un flux négatif pour la banque. Les deux flux de 6 000 € sont des flux positifs.

Un échéancier peut être utilisé pour représenter des flux se produisant à tout moment de l’année ; il suffit pour ce faire de changer la définition de la longueur d’une période (de l’année au mois ou au jour). La plupart des diagrammes de flux de ce chapitre sont très simples, au point de paraître inutiles. Cependant, plus les problèmes se compliquent, plus le recours à un diagramme des flux est utile pour ne pas risquer d’oublier des flux.

 

Application 1

Construction d’un échéancier des flux

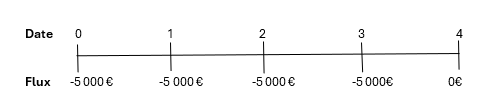
Les frais de scolarité d’une grande école de commerce sont de 10 000 € par an. La scolarité dure deux ans. Les paiements doivent être effectués à parts égales à chaque début de semestre. Quel est le diagramme des flux ?

 

Solution

Si l’on considère que le premier semestre débute aujourd’hui, le premier versement a lieu à la date 0. Les paiements suivants sont espacés d’un semestre. Le diagramme des flux est :

 

                                                                                                                                                                                                               

      

 

2-    Les déterminants des taux d’intérêts

 

Fondamentalement, les taux d’intérêt sont déterminés sur les marchés financiers par la confrontation entre l’offre et la demande de capitaux. Mais cette offre et cette demande sont elles-mêmes influencées par de nombreux facteurs macroéconomiques (inflation, croissance anticipée…) et microéconomiques (le risque ou la fiscalité de l’emprunteur).

 

2.1.         Taux d’intérêt nominal et réel

 

Le taux d’intérêt est le prix (ou le coût) que doivent payer les agents économiques qui bénéficient d’un emprunt (ou crédit), et c’est aussi le prix (ou la rémunération) que reçoivent les agents économiques qui ont accordé un prêt (ou dépôt). Le taux d’intérêt s’exprime généralement en pourcentage, le plus souvent en pourcentage annuel.

Pour comprendre le rôle des taux d’intérêt dans l’économie, il convient de distinguer également le taux d’intérêt nominal et le taux d’intérêt réel en prenant en compte l’inflation.

L’intérêt nominal d’un placement correspond au taux inscrit dans le contrat. Cependant, en cas d’inflation, l’intérêt nominal est différent de l’intérêt réel, c’est-à-dire de ce que le placement rapporte véritablement, une fois l’inflation prise en compte. Pour connaître le taux d’intérêt réel d’un placement, on peut, en première approximation, retrancher le taux d’inflation du taux d’intérêt nominal.

Pour un agent économique emprunteur, sa capacité à rembourser un crédit dépend du taux d'intérêt nominal, par exemple, rembourser un crédit à 10 % coûte plus cher qu'à 5 %. De plus, le taux d'inflation influence ce coût : emprunter à 10 % avec une inflation de 8 % n'est pas équivalent à emprunter à 10 % avec une inflation de 2 %. Il est donc crucial de considérer le coût réel d'un emprunt, qui relativise le coût en fonction du pouvoir d'achat de la monnaie dans le temps.

La distinction entre taux d’intérêt nominal et taux d’intérêt réel est cruciale pour mesurer le rendement réel de l’épargne pour l’agent économique prêteur,

Le taux d’intérêt nominal est le taux effectivement convenu par contrat et effectivement payé. Il repose sur un raisonnement à prix courants, soit ceux de la période observée.

Le taux d’intérêt réel, quant à lui, est égal au taux d’intérêt nominal moins le taux d’inflation.

L’inflation est l’augmentation générale du niveau des prix qui aboutit à une perte de pouvoir d’achat de la monnaie. Quand l’inflation est significative, 1.000€ prêtés aujourd’hui n’auront pas le même pouvoir d’achat lors de leur remboursement dans un an.

La relation qui lie le taux d’intérêt nominal r, le taux d’intérêt réel r_r et le taux d’inflation π est connue sous le nom de relation de Fischer :

   

 

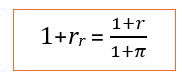
On peut modifier cette équation afin d’exprimer le taux d’intérêt réel en fonction du taux nominal et du taux d’inflation, avec une approximation utile quand l’inflation est faible :

Taux d’intérêt réel

 

 

 

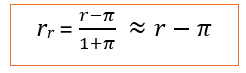
 Autrement dit, le taux d’intérêt réel est approximativement égal au taux d’intérêt nominal moins le taux d’inflation. On ne doit pas recourir au taux d’intérêt réel pour actualiser les flux futurs, à moins que ceux-ci ne soient eux-mêmes exprimés en termes réels, c’est-à-dire corrigés de l’inflation. Dans tout cet ouvrage, les flux sont exprimés en termes nominaux ; il convient donc de les actualiser avec un taux d’intérêt nominal.

 

2.2.         Illustration

 

 

 

             

En cas d’inflation, le prêteur cherchera à incorporer cette perte de pouvoir d’achat dans le taux nominal qu’il demande.

 

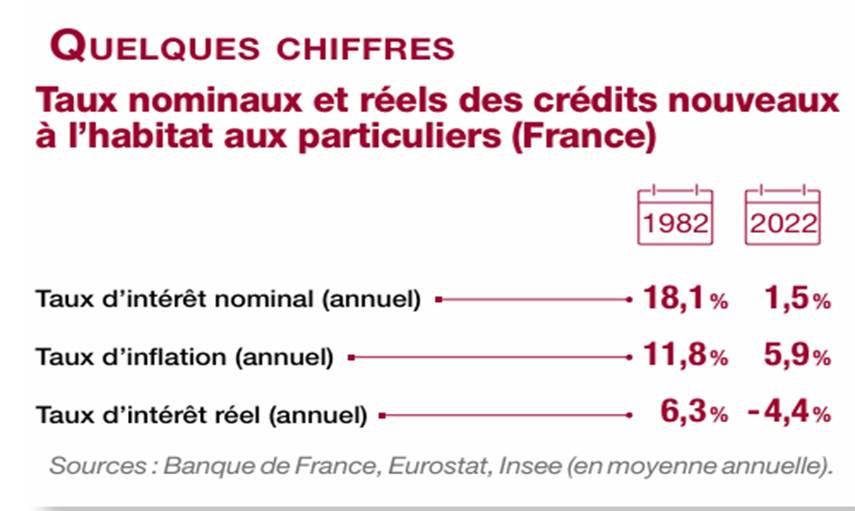
Taux d’intérêt réel – cas pratique

 

Première situation – Inflation faible

Soit un prêt d’une durée de 1 an, au taux de 7,1% et un taux d’inflation prévu pour l’année à venir de 2%.

Le taux d’intérêt réel r = (1+0,071) / (1+0,02) -1 = 0,05 = 5%

La différence 7,1% - 2% = 5,1% est une bonne approximation du calcul.

 

Deuxième situation – Inflation forte

Soit un prêt d’une durée de 1 an à un taux d’intérêt de 32%, et un taux d’inflation prévu pour l’année à venir qui est de 10%.

Le taux d’intérêt réel r = (1+0,32) / (1+0,1) – 1 = 0,2 = 20%

Cette fois la différence 32% - 10% = 22% n’est pas une bonne approche car, elle surestime fortement le taux d’intérêt réel qui n’est que de 20%.

 

3-    Taux d’intérêt simple

L’intérêt simple est la somme payée par un emprunteur à un prêteur pour l’usage de son capital pendant une période déterminée (somme due au créancier par son débiteur en rémunération d'un prêt). C’est le loyer de la somme prêtée. Le taux d’intérêt simple est l’intérêt que rapporte une unité monétaire pendant une période, en générale une année.

L’intérêt simple ne s’ajoute pas au capital pour porter lui-même intérêt. L’intérêt simple est proportionnel au capital prêté ou emprunté. Il est versé en une seule fois au début de l’opération, c’est-à-dire lors de la remise du prêt, ou à la fin de l’opération c’est à dire lors du remboursement. L’intérêt simple concerne essentiellement les opérations à court terme (inférieures à un an).

L’intérêt simple est calculé en fonction : Du capital prêté C, de la durée de la période n, du taux d’intérêt simple i

I = C x i x n

 

Observations 

Si la durée du placement est estimée en mois, on aura : I = C x i x n/12

Si la durée du placement est estimée en jour, on aura :   I = C x i x n/360

Lorsque la durée de placement est exprimée en jours, l’intérêt est calculé sur la base de l’année financière ou commerciale comptant 360 jours. Dans le cas d’une année civile, l’intérêt est calculé sur la base de de 365 jours. Les mois sont comptés à leur nombre exact de jours, et on ne tient compte que de l’une des deux dates extrêmes. 

Exemple

Un capital de 38000 € est placé à intérêt simple au taux annuel de 8% du 22 mars au 10 septembre. Déterminez l’intérêt simple produit par le capital.

Résolution

L’on détermine d’abord la durée du placement en nombre de jour. 

Mars : 31 – 22 = 9 jours (l’on exclut la date initiale)

Avril : 30 jours

Mai : 31 jours

Juin : 30 jours

Juillet : 31 jours

Août : 30 jours

Septembre : 10 jours (l’on inclut la date finale).

N = 171 jours

I = 38000 € x 0.08 x 171/360

I = 1444 €

 

4-    Taux d’intérêt proportionnel

 

A partir d’un taux d’intérêt annuel on peut calculer le taux d’intérêt proportionnel pour une période différente.

Taux proportionnel = Taux annuel × Durée de la période / Durée de l'année.

 

Exemple : Taux proportionnel mensuel pour un taux annuel de 6% : 0,06 x 1 mois / 12 mois = 0,50%

Taux proportionnel pour la période du 1/1/2020 au 15/2/2020 pour un taux annuel de 10% : 0,10 ×46 jours / 365 jours = 1,26%.

N.B : Avant de faire vos calculs, vérifiez quel est le nombre de jours bancaires applicable, qui varie selon les pays.

 

5-    Taux d’intérêt composé

 

Un capital est dit placé à intérêt composé, lorsqu’à l’issue de chaque période de placement, les intérêts sont ajoutés au capital pour porter eux même intérêts à la période suivante au taux convenu. On parle alors d’une capitalisation des intérêts. Cette dernière opération est généralement appliquée lorsque la durée de placement dépasse un an. La capitalisation permet aux intérêts eux-mêmes de générer des intérêts supplémentaires pendant la durée restante du prêt. Ainsi, le montant total à rembourser augmente, entraînant un effet d'accumulation sur le capital.

On a donc pour la période 1 :

C1 = C0 + i

= C0 + (C0i)

= C0 (1+i)

Pour la deuxième période, le capital initial est le capital de départ C0 augmenté des intérêts de la période 1 : c'est donc C1

On a donc pour la période 2 :

C2 = C1 x i

= C0 (1+i) x (1+i)

= C0 (1+I) ²

 

 

Application

Vous décidez d'investir un capital de 1 000 € dans un compte d'épargne qui offre un taux d'intérêt composé de 5 % par an. Vous souhaitez savoir combien d’intérêts vous avez produit après 2 ans.

Il vous suffit de poser la formule suivante :

I= capital initial (C0) X (1+i) ²) –C0, 

I = 1000 X (1+0,05) ² - 1000

I = 102,5

Après n périodes, la méthode des intérêts composés est la suivante :

 

C_n = C₀ (1+i) ⁿ

 

Où C₀ est la valeur initiale et C_n la valeur finale. Ces valeurs correspondent respectivement à ce qu’on appelle en finance la valeur actuelle et la valeur future.

 

 

6-    Valeur Actuelle (VA)

 

La valeur actuelle correspond à la valeur d’un flux de trésorerie espéré transposé dans le passé.

Ainsi, pour transposer un flux dans le passé, il faut l’actualiser.

Si l’on désire connaître la valeur aujourd’hui de 1 000 € à recevoir dans un an et que le taux d’intérêt soit de 10 %, il est possible de procéder de la manière suivante :

(1000 € dans un an) / (1,1 € dans un an par euro aujourd’hui) = 909,09 € aujourd’hui

Pour transposer un flux dans le passé, il faut le diviser par le facteur de taux d’intérêt, (1 + t), avec t le taux d’intérêt. Le procédé consistant à transposer dans le passé un flux (en calculant la valeur à la date d’aujourd’hui de ce flux survenant dans le futur) est appelé actualisation (discounting).

Afin d’illustrer cette règle, supposons qu’un agent anticipe de recevoir 1 000 € dans deux ans. Si le taux d’intérêt annuel est de 10 % pour les deux prochaines années, l’échéancier est :

                          

  

 

                                        

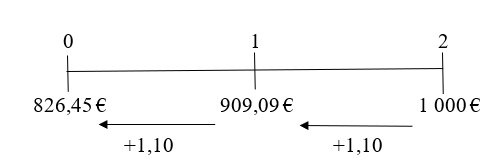
Avec un taux d’intérêt de 10 %, tous les flux (826,45 € à la date 0 ; 909,09 € à la date 1 ; 1 000 € à la date 2) sont équivalents. Les flèches vers la gauche indiquent que les flux sont transposés dans le passé, c’est-à-dire actualisés. La valeur actuelle de 1 000 € à recevoir dans deux ans est donc égale à 826,45 €.

Plus généralement, pour transposer un flux F jusqu’à un point n périodes avant qu’il ne se produise, il faut l’actualiser n fois. Cela signifie qu’il faut diviser le flux F par n facteurs de taux d’intérêt. Si le taux d’intérêt t est constant :

Valeur actuelle d’un flux

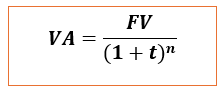
VA = Valeur actuelle

FV = Valeur future (flux de trésorerie futur)

t = Taux d'actualisation (taux d'intérêt)

n = Nombre de périodes jusqu'à la réception du flux de trésorerie.

 

7-    Valeur Future (FV)

 

La valeur future (FV) quant à elle, est la valeur d'un fux après un certain temps. Elle calcule combien un montant investi aujourd'hui vaudra à l'avenir. Calculer la valeur future d’un flux, revient à transposer ce flux dans le futur. La valeur d’un flux transposée dans le futur est qualifiée de valeur future (ou valeur à terme, ou valeur acquise).

On dispose de 1 000 € aujourd’hui. On désire déterminer le montant équivalent à cette somme dans un an. Si le taux d’intérêt est de 10 % sur le marché, il est possible d’utiliser ce taux d’intérêt comme un taux de conversion (un taux de change) pour transposer les flux dans le futur :

(1000 € aujourd’hui) x (1,1 € dans un an pour un € aujourd’hui) = 1100 € dans un an

De manière générale, si le taux d’intérêt annuel est t, il est possible de multiplier un flux intervenant en début d’année par le facteur de taux d’intérêt (1 + t) pour le transposer en fin d’année. On peut appliquer cette règle plusieurs fois d’affilée. Pour calculer la valeur dans deux ans de 1 000 € reçus aujourd’hui, si le taux d’intérêt la seconde année est toujours de 10 % :

(1100 € dans un an) x (1,1 € dans deux ans par euro dans un an) = 1210 € dans deux ans

L’échéancier est :

 

                      

 

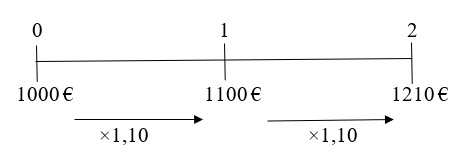
Avec un taux d’intérêt de 10 %, tous les flux (1 000 € à la date 0 ; 1 100 € à la date 1 ; 1 210 € à la date 2) sont équivalents. Ils sont cependant exprimés dans des unités différentes, puisqu’ils se produisent à différents moments. Les flèches vers la droite indiquent que les flux sont transposés dans le futur.

Dans l’exemple ci-dessus, 1 210 € est la valeur future de 1 000 € dans deux ans. La différence entre la valeur future d’un flux et sa valeur actuelle traduit la valeur temps de l’argent : en disposant de l’argent plus tôt, on peut le placer, en tirer des intérêts et obtenir ainsi plus d’argent à l’avenir.

On remarque par ailleurs que la valeur future augmente de 100 € la première année et de 110 € la seconde. La seconde année, les intérêts gagnés sont calculés sur les 1 000 € de départ mais également sur les 100 € d’intérêts reçus à la fin de la première année. Lorsque les intérêts portent eux-mêmes intérêts (ce qui est le cas dans cet exemple), on parle d’intérêts composés (autrement, on parle d’intérêts simples). Le procédé visant à transposer des flux dans le futur s’appelle la composition ou capitalisation des intérêts.

La formule de la Valeur future d’un flux est donnée par : 

 

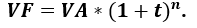
Application 1 valeur actuelle et future

Prenons le cas d’une entreprise qui prévoit de recevoir 100 000 € dans 1 an. Supposons que le taux d'actualisation est de 5 %.

Appliquons la formule :

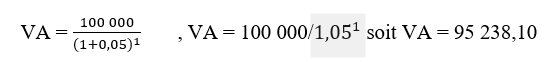
Prenons à présent le cas de cette entreprise qui souhaite connaitre la valeur à terme d’une somme de 100 000 € placée aujourd’hui pour 1 an à un taux de 5%.

 

 

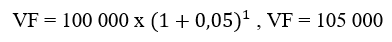
8-    Valeur actuelle nette d’une séquence de flux

 

Un projet peut être représenté sur un échéancier comme une séquence de flux, où les sorties d’argent (les dépenses et investissements) sont des flux négatifs et où les entrées d’argent (les recettes) sont des flux positifs. La VAN d’un projet est la différence entre les valeurs actuelles (VA) de ses bénéfices et de ses coûts :

 

Valeur actuelle nette

VAN = VA (Bénéfices) – VA (Coûts)

 

Si les flux sont exprimés sous forme algébrique, autrement dit si les bénéfices sont affectés d’un signe « + » et les coûts d’un signe « – », la VAN est simplement la somme des valeurs actuelles de tous les flux et futurs :

 

VAN = VA (Ensemble des flux de l’investissement)

 

Si un titre vous verse une série de flux annuels on actualisera les flux de chaque année pour calculer la valeur actuelle comme suit :   

 

 

 

 

 

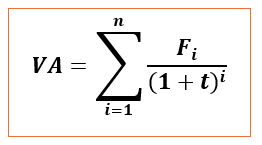
Fi : Flux généré par le titre

t : taux d’actualisation

i : années

Si vous pouvez acheter ce titre aujourd’hui pour une valeur on calculera la valeur actuelle nette (VAN) comme étant la différence entre la valeur actuelle et la valeur de marché.

 

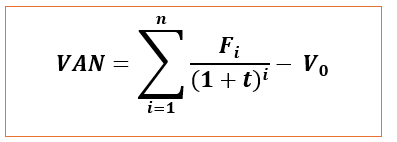
Application 2

Un investissement promet 4 flux annuels de 52€ sur les 4 prochaines années. Sachant que vous exigez un taux de rentabilité de 8% quel est son juste prix ?

Solution :

TAUX	8%
Année	1	2	3	4
Flux €	52	52	52	52
Coefficient d'actualisation	0,925926	0,857339	0,7938322	0,735030
Valeur actuelle €	48,15	44,58	41,28	38,22
Somme 1 à 4	172,23

 

Si vous pouvez l’acheter à 170€, alors la VAN de votre investissement sera positive de 2,23€ (172,23 –170).

 Si en revanche le titre cote 175€, la VAN est négative et vous ne ferez probablement pas cet investissement.

 

II-         ANNUITES

 

 

L’on désigne par annuité, une suite de règlements effectués à intervalles de temps régulier pendant une certaine durée. Cette suite de règlements (ou termes) constitue une rente pour celui qui en bénéficie. L’intervalle de temps séparant deux versements est une période. En fonction de l'intervalle de temps, on aura donc des annuités, mensualités ou toute autre périodicité (sur un trimestre, semestre, etc.).

L’Annuité représente le montant total que les emprunteurs devront rembourser chaque année, comprenant à la fois une part du capital et les intérêts.

 

1-    La valeur future ou acquise par une suite d’annuités de fin de période.

A la fin de chaque période on procède au versement d’une annuité « a ». On cherche à calculer la valeur acquise « Va » à la fin du placement, et ce en tenant compte d’un taux d’intérêts composés « i ».

 

 

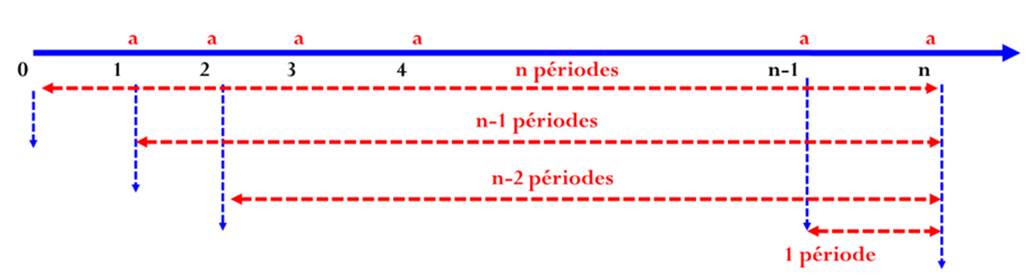
Si on note par :

§ Vn : la valeur acquise par la suite des annuités

§ a : l’annuité constante de fin de période

§ n : le nombre de périodes (d’annuités)

§ i : le taux d’intérêt par période de capitalisation

 

On a :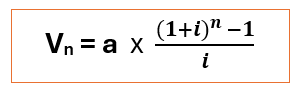 

Applications :

1/ Une entreprise s’est endettée auprès de sa banque et doit verser une suite de 10 annuités d’un montant de 150.000 € chaque année. Sachant que le taux d’intérêt pratiqué est de 9% l’an, déterminer la valeur acquise lors du dernier versement.

2/ Déterminer le montant qu’il faut verser à la fin de chaque trimestre pendant une durée de 9 ans, pour constituer à la date du dernier versement, un capital de 450.000€ sachant que le taux trimestriel est de 2%.

Corrigés :

1/ Valeur acquise lors du dernier versement :

 

 

 

 

2/ Montant trimestriel à verser :

 

 

 

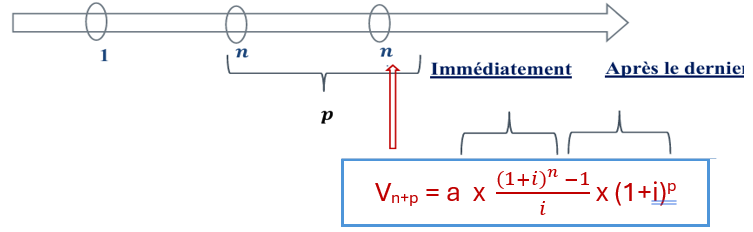
1.1- Valeur acquise à une date postérieure au dernier versement

Si on note par

§ Vn : la valeur acquise par la suite des annuités

§ a : l’annuité constante de fin de période

§ n : le nombre de périodes (d’annuités)

§ p : le nombre de périodes après de le dernier versement

§ i : le taux d’intérêt,

 

  

La valeur acquise de n annuités de p périodes après le dernier versement est :

 

  

 

 

 

Application :

Une entreprise place 10.000€ le 31/12 de chaque année au cours des années N à N+9 incluse au taux d’intérêt annuel de 3%. Les intérêts continuent à courir après cette date.

*De combien disposera l’entreprise juste après le dernier versement ?

*De combien disposera l’entreprise le 01/01/N+13.

Corrigé :

De combien disposera l’entreprise juste après le dernier versement ?

 

 

 

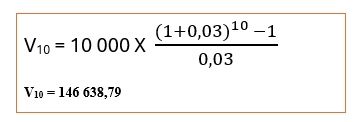
De combien disposera l’entreprise le 01/01/N+13 ?

 

 

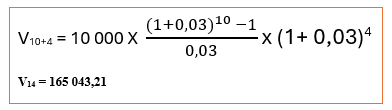
 1.1- La valeur acquise par une suite d’annuités de début de période.

 

Dans de le cas des annuités de début de période, les versements ont lieu au début de chaque période. La valeur Acquise des annuités constantes de début de période s’obtient suivant la formule suivante :

 

 

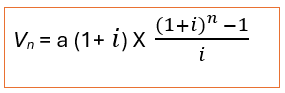
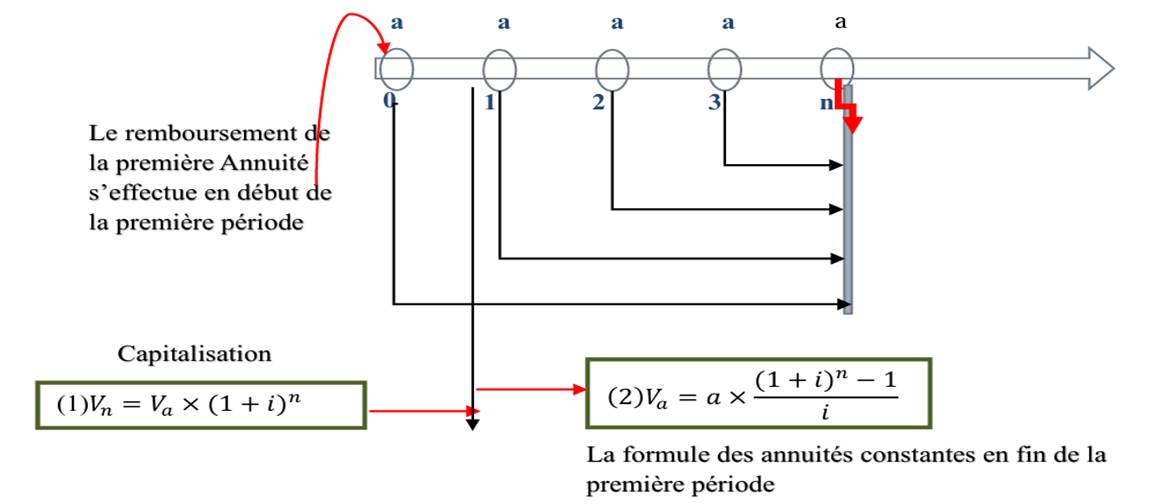
Application

1/ Calculer le capital constitué un an après le dernier versement, par une suite de 12 annuités de 27 500 € chacune. Taux : 9% l’an.

2/ Quel doit être la valeur de 6 placements égaux effectués, au début de chaque trimestre pour avoir une valeur acquise de 18 790,98 €, si le taux annuel est de 5% ?

 

Corrigé :

1/ Capital constitué un an après le dernier versement :

 

 

 

2/ Valeur de 6 placements égaux :

 

On commence d’abord par le calcul du taux d’intérêt de la période considérée (trimestre),   

 

  

 

 

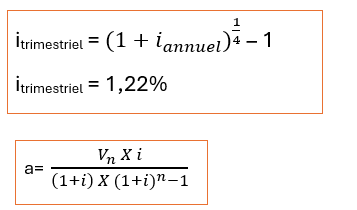
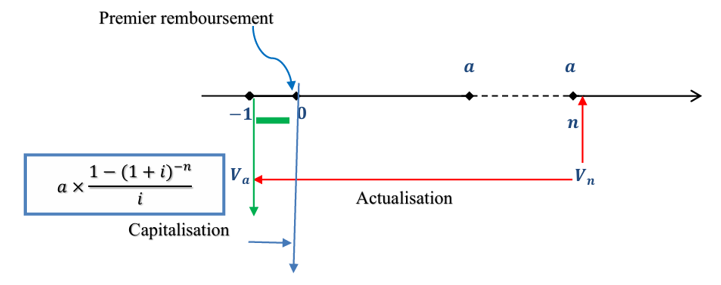
2- La valeur actuelle d’une suite d’annuités de fin de période

 

On appelle valeur actuelle d’une suite d’annuités constantes de fin de période, la somme des annuités actualisées (V0) exprimée à la date origine.

Si on note par :

§ V0 : la valeur actuelle de la suite des annuités

§ a : l’annuité constante de fin de période

§ n : le nombre de périodes (d’annuités)

§ i : le taux d’intérêt par période d’actualisation

 

 

 

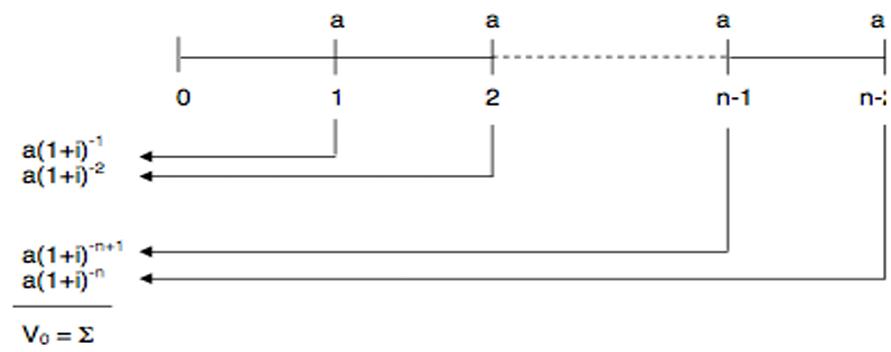
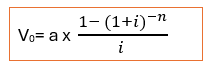
Exemple : Déterminer la valeur actuelle d’une suite d’annuités constantes de 1500€ versées à la fin de chaque année pendant 8 ans. Le taux est 10%.

 

  

 

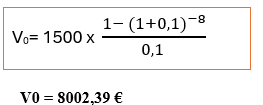
 2.1- La valeur actuelle d’une suite d’annuités de début de période

 

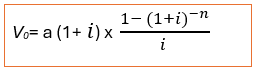
Application :

Calculer la valeur actuelle, au moment du versement du premier terme, par une suite de 15 annuités de 31.000 € chacune. Taux d’intérêt : 12,5% l’an.

Corrigé :

  

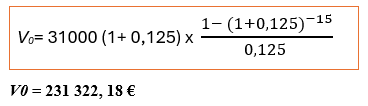
 2.2- L’équivalence de capitaux

 

      Elle consiste à remplacer une suite d’annuités par un montant unique, ce qui nécessite l’évaluation de la suite à une date quelconque.

 

Application :

Pour acheter une voiture de fonction, un jeune entrepreneur est face à deux possibilités :

1. Règlement en 8 annuités constantes, de 30.000€ chacune.

2. Règlement en un versement unique, dans 4 ans, après la date d’acquisition.  Sachant que le taux d’intérêt est de 11%, déterminer la valeur nominale du versement unique ?

 

 

Solution :

1. Pour un règlement en 8 annuités constantes, de 30.000€ chacune on aura :

 

 

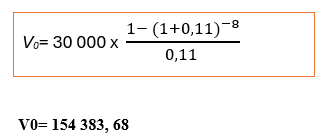
2. Règlement en un versement unique, dans 4 ans, on aura :

 

 

  

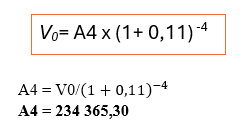
Le montant du versement unique dans 4 ans, équivalent aux 8 annuités de 30 000 €, serait d'environ 234 365, 30€. Cela permet à l'emprunteur de choisir la méthode de paiement qui lui convient le mieux, tout en prenant en compte le coût de l'argent dans le temps.

 

 

 

 

III-     EMPRUNTS INDIVIS

 

Un emprunt indivis est un emprunt contracté auprès d’un seul prêteur. Dans le processus de remboursement d’un emprunt indivis, on subdivise le temps en parties égales appelées périodes. La période peut être l’année, le semestre, le trimestre…

 

1- Caractéristiques d’un emprunt indivis

 

L’emprunteur du capital s’engage à s’acquitter de sa dette (capital et intérêt) de sorte que les sommes versées pour le remboursement soient équivalentes au capital emprunté augmenté des intérêts dus.

Le remboursement d’un emprunt est composé de deux parties :

•        L’amortissement qui est la somme destinée à rembourser au prêteur le capital emprunté ;
•        L’intérêt qui est la somme destinée à rémunérer le prêteur pour le service de la dette.

L’emprunt indivis peut être remboursé de deux façons :

•         Par amortissements constants ;
•         Par annuités constantes.

 

Un emprunt indivis est caractérisé par :

• Le montant de la dette (dette initiale ou valeur nominale) 𝑫_𝟎

• La durée 𝒏 de l’emprunt souvent assimilée au nombre d’échéances

• L’intérêt 𝒊 de 1 unité monétaire pour une période.

 

 

 3- Tableau général de remboursement

 

On note par 𝑫_𝒑−𝟏 la dette au début de la 𝒑^{𝑖è𝑚𝑒} période, 𝑰_𝒑 l’intérêt de la période p, 𝒎_𝒑 l’amortissement de la 𝒑^{𝑖è𝑚𝑒} période, 𝒂_𝒑 le versement en fin de la 𝒑^{𝑖è𝑚𝑒} période, 𝑫_𝒑 la dette restante due immédiatement après le 𝒑^{𝑖è𝑚𝑒} versement.

(1 ≤ 𝑝 ≤ 𝑛)

En supposant que le premier versement à lieu une période après que la dette ait été contractée, on a à titre indicatif le tableau suivant :

 

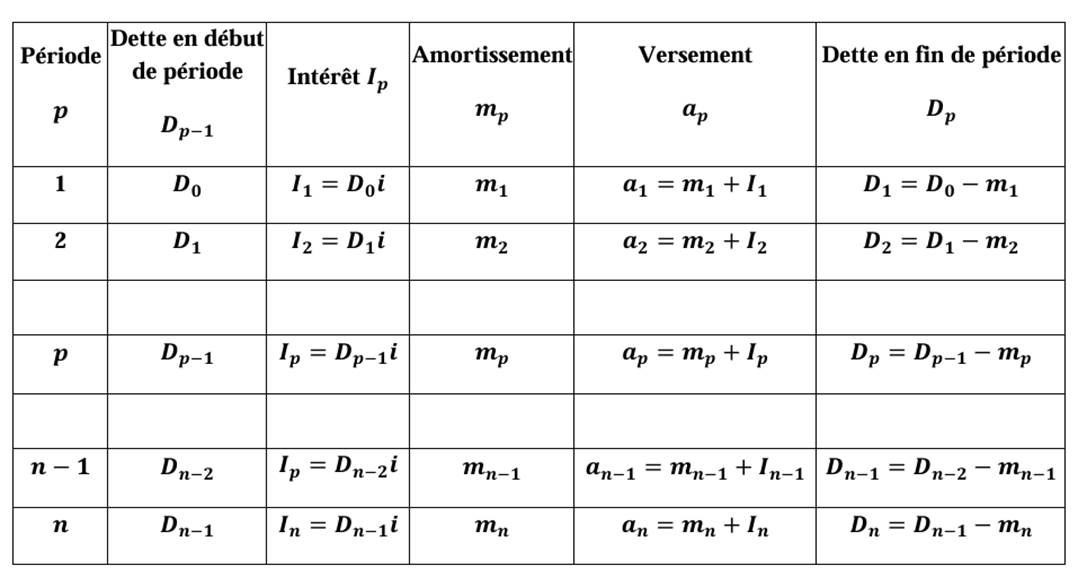
Exercice : Une dette de 12 000 € est remboursable au moyen de cinq versements semestriels le premier venant un semestre après que la dette a été contractée. Les amortissements contenus dans les versements sont, par ordre chronologique, 4 000 €, 2 000 €, 3 000 €, 2 500 € et un montant 𝒎. Le taux annuel de remboursement étant de 10,25%.

1) Calculer le taux semestriel 𝒊 équivalent au taux annuel 𝒊𝒂 de 10,25%

2) Calculer 𝒎

3) Présenter le tableau d’amortissement de cet emprunt.

Résolution

1) Calcul du taux semestriel

I =  = 5%

2) Détermination du montant m

M = 12000 – (4000 + 2000 + 3000 + 2500) = 500

3) Le tableau d’amortissement

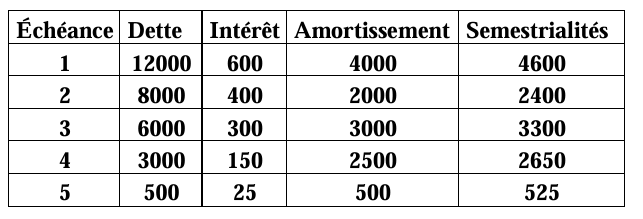
4-    Remboursement par versements périodiques constants

Ici, 𝒂𝟏=𝒂𝟐=⋯=𝒂𝒑=⋯=𝒂𝒏= a et on démontre que :

 

 

 

D₀ étant la dette initiale.

 

 

 

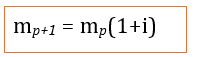
Les amortissements sont en progression géométrique et on a finalement plusieurs façons de trouver l’annuité.

A titre indicatif, on a le tableau suivant :

 

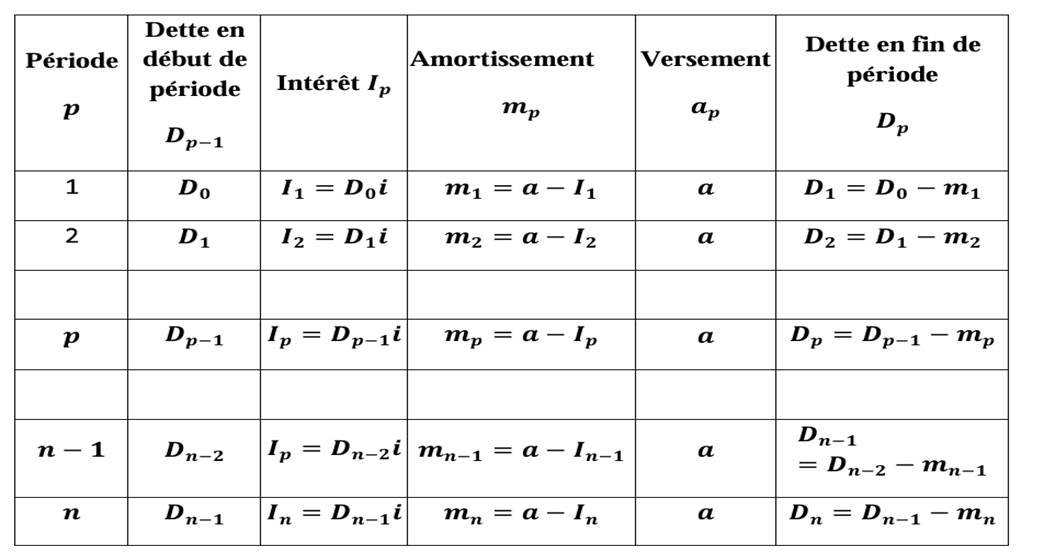
Exercice :

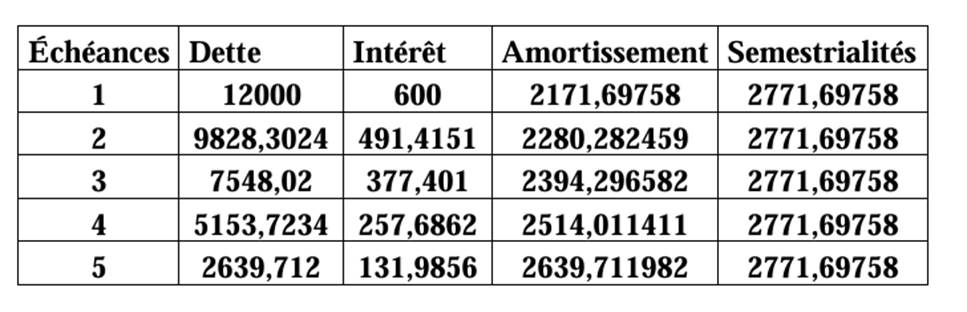
Une dette 𝑫 est remboursable au moyen de cinq versements semestriels constants, le premier d’un montant de 2 771, 69758 € venant un semestre après que la dette ait été contractée. Le premier amortissement étant de 2 171, 69758

1) Calculer le taux semestriel 𝒊 et le taux annuel équivalent 𝒊𝒂.

2) Calculer 𝑫

3) Présenter le tableau d’amortissement de cet emprunt.

Résolution

1)      Calcul du taux semestriel et du taux annuel

*Déterminons l’intérêt

 I = 2771,69758 - 2171,69758 = 600

 *Déterminons le taux semestriel i :    

 

 

           Déterminons le taux annuel :   

 

 

 

 

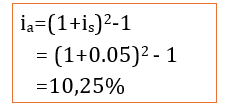
2)      Déterminons la dette Do

 

 

 

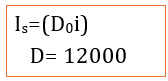
3)      Tableau d’amortissement

 5- Remboursement par amortissement constants

Dans le cas d’un amortissement périodique ou constant, le rapport entre la dette initiale et la durée de vie de l’emprunt vous donne l’amortissement à verser chaque année.

 

 

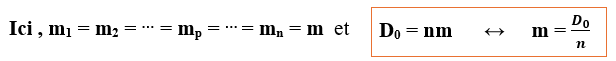
On démontre que :   

 

 

 

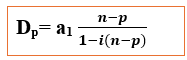
et on peut avoir plusieurs façons de calculer les amortissements comme suit :

 

    a_n = m + I_n;       a_n = m + m_i ;      a_n = m(1+i)

 

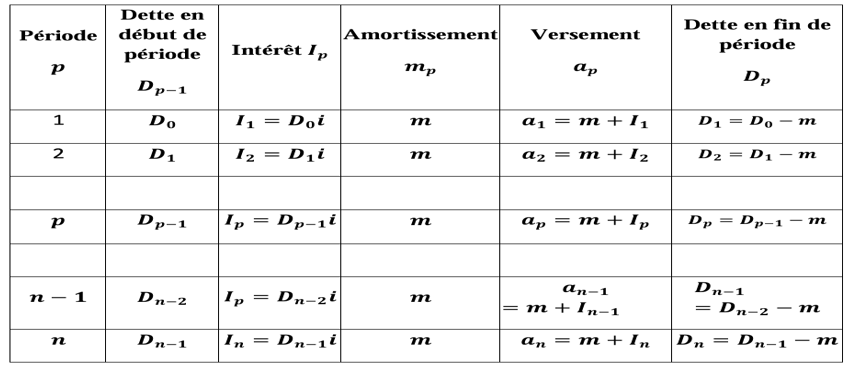
A titre indicatif, on a généralement le tableau suivant pour ce cas :

 

 

Exercice :

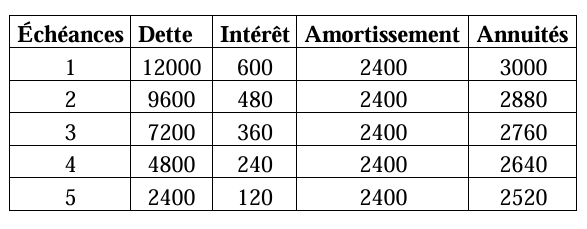
Une dette de 12 000 € est remboursable au moyen de cinq versements semestriels le premier venant un semestre après que la dette a été contractée. Les amortissements contenus dans les versements sont constants de montant 𝒎. Le taux annuel de remboursement étant de 10,25%.

1) Calculer le taux semestriel 𝒊 équivalent au taux annuel 𝒊𝒂 de 10,25%.

2) Calculer 𝒎.

3) Présenter le tableau d’amortissement de cet emprunt.

 

 

Résolution :

 

1)              Calcul du taux semestriel

I = (1 + 0.1025) ^1/2 - 1

I = 5%

 

2)              Calcul de m

                m = 12000/ 5  

                m = 2400

 

 

3)              Tableau d’amortissement

 6- Remboursement en block

Ici il y a essentiellement deux modes : L’un, les intérêts périodiques sont payés mais on ne procède à aucun amortissement avant la fin du contrat d’emprunt. A la fin de la dernière période, on paye le dernier intérêt et on rembourse intégralement la dette. L’autre, on ne paye pas d’intérêt et on ne rembourse rien avant la fin du contrat. A la fin de la dernière période, on paye les intérêts générés pendant la durée de l’emprunt et on rembourse intégralement la dette.

 

Exercice :

 Une dette de 12 000 € est remboursable en un seul block. L’emprunt a une durée de 5 ans.

1) En supposant qu’on paye seulement les intérêts chaque fin de période et que le montant global de ces intérêts est de 6 150 €, calculer le taux annuel d’intérêt et présenter le tableau d’amortissement.

2) On suppose maintenant qu’aucune somme n’est payée avant la fin de la dernière année. L’intérêt global étant 6 150 €, calculer le taux annuel d’intérêt et présenter le tableau d’amortissement.

 

 

Résolution :

• Montant de la dette : 12 000 €
• Durée : 5 ans
• Intérêts globaux : 6 150 €

1)     Paiement des Intérêts à la Fin de Chaque Période

Intérêt annuel = 6150/5

                        = 1230 €

Taux d’intérêt = 1230/12000

                        = 0,1025 soit 10,25%

 

Tableau d’amortissement

 

 

2)    Aucune somme payée avant la fin de la dernière année

Total des paiements à la fin de la période = 12000+6150= 18 150

Calcul du taux d'intérêt :  

=18150​/12000≈1,5125

1+i = ≈1,0860

i ≈ 0,0860 soit 8,60%

 

  

Tableau d’amortissement

 

 

 

 

 

IV-      LES RENTES PERPETUELLES

Une rente perpétuelle (perpetuity) est un titre de dette qui prévoit le paiement régulier d’intérêts mais pas le remboursement du capital ; une rente perpétuelle n’a donc théoriquement pas de terme. En pratique, elle s’achève lorsque l’emprunteur fait faillite ou décide de racheter tous les titres en circulation sur le marché. L’émission de nouveaux titres de rente perpétuelle est rare sur les marchés, mais comprendre la façon dont on les évalue est utile.

On suppose maintenant un versement fixe annuel qui ne s’arrête jamais. La rente perpétuelle est souvent utilisée comme une approximation pour des situations qui n’ont pas de fin prévisible. La valeur actuelle (VA) d’une rente perpétuelle s’exprime par la formule simple suivante :

 

 

 

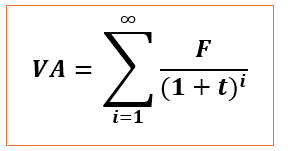
En faisant tendre n vers l’infini on obtient :

 

 

 

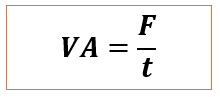
Exemple :

La valeur actuelle à 10% d’un flux annuel infini de 100€ est donc de : VA= 100/10% = 1000€

Une rente de 100€ à 10% vaut 1000€ en valeur d’aujourd’hui. Si le taux exigé par l’investisseur est de 20%, cette rente vaut alors 500€.

 

Perpétuité croissante

Si maintenant le flux de référence F croit de g par an jusqu’à l’infini on aura alors :

À condition que t > g

 

 

 

 

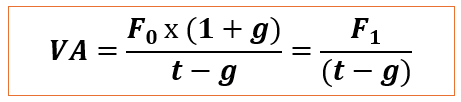
C’est la formule de Gordon-Shapiro

 

Par exemple un titre financier rapportant un flux en année 1 de 8€ croissant à l’infini de 5% par an, a une valeur actuelle au taux de 10% de :

 

VA = 8 / (0,1- 0,5) = 160

 

 

Exercice pratique : construisez la table des valeurs pour un flux de départ de 10€, avec les taux d’actualisation 5%, 10%, 15%, 20% et les taux de croissance 2%, 5%, 10%, 15%.

 

Question de réflexion : dans quelles situations et pour quel type de sociétés Gordon-Shapiro ne sera pas applicable ?                                                                                                                   

 

Application de Gordon-Shapiro

Les actionnaires d’Alpha estiment que ses résultats ainsi que son dividende devraient doubler en 5 ans. La rentabilité exigée est de 20% et le dernier dividende versé est 5 euros par action. Quelle est la valeur de l’actions ?

Calculons d’abord le taux de croissance des dividende g.

Partant de D₀, le dividende actuel, nous savons que D₅, dividende dans 5 ans doit doubler.

                   

On a donc                                 D₅=2D₀

Ou aussi                                    (1+g)⁵D₀ = 2D₀

Ce qui nous donne                    g = 0,1487

 

Le taux de croissance des dividendes est donc égal à 14,87% pour les cinq prochaines années. En supposant que ce taux de croissance est perpétuel nous appliquerons la formule de Gordon et Shappiro.

La valorisation théorique de l’action sera alors :

 

Soit                        P = 111,96€

Refaites le calcul pour un doublement du dividende en 10 ans.

 

 

------

 

CONCLUSION  

 La valeur temps de l'argent est un concept essentiel en finance qui souligne l'importance du timing dans la gestion des flux financiers. Les outils étudiés, comme les taux d'intérêt, la valeur actuelle et future, les annuités et les rentes perpétuelles, permettent d'optimiser la création de valeur à long terme, en tenant compte de l'inflation et de la puissance des intérêts composés.

     La maîtrise de ces principes est cruciale pour prendre des décisions financières éclairées, que ce soit pour la planification d'investissements, la gestion de la dette ou l'évaluation d'actifs.