PLAN DU COURS

INTRODUCTION

Dans un monde financier en perpétuelle évolution, marqué par des incertitudes croissantes et des marchés de plus en plus interconnectés, la compréhension des concepts de risque et de rendement s’impose comme un pilier essentiel pour tout investisseur ou décideur financier.

Le risque, souvent perçu comme la probabilité de subir une perte ou de ne pas atteindre les objectifs fixés, est indissociable du rendement, qui représente la récompense espérée pour avoir pris ce risque. Ensemble, ils forment le cœur de la prise de décision financière, influençant les stratégies d’investissement, la gestion de portefeuille et même les politiques économiques.

Dans un contexte de tensions géopolitiques, de fluctuations des taux et de technologies émergentes comme l’IA, la gestion du risque et du rendement est essentielle. Les investisseurs doivent concilier opportunités de rendement et risques systémiques, climatiques ou cybernétiques. Une approche équilibrée est cruciale pour naviguer dans des marchés volatils et interconnectés.

Ce cours se propose d’explorer en profondeur les fondements théoriques et pratiques de la gestion du risque et du rendement. Nous aborderons les mesures traditionnelles telles que la densité de probabilité, la rentabilité espérée, et l’écart-type, tout en intégrant des outils modernes comme la Value at Risk (VaR). Nous plongerons également dans la théorie de portefeuille, en calculant le rendement et le risque dans un tel contexte et en examinant comment la diversification peut réduire le risque spécifique, tout en mesurant le risque systématique à travers le Modèle d’Equilibre des Actifs Financiers (MEDAF). Enfin, nous évaluerons les performances ajustées au risque à l’aide de ratios tels que celui de Sharpe ou de Sortino, et nous explorerons les techniques d’optimisation de portefeuille.

 

MESURES TRADITIONNELLES DU RISQUE ET DE LA RENTABILITE

                                                                                      

Lorsqu’un entrepreneur décide d’investir dans un projet ou qu’un investisseur achète un actif financier, ils ont une certaine vision des risques et de la rentabilité qu’ils en attendent. Comment mesurer ces deux grandeurs ?

BON A SAVOIR : Différence entre une population et un échantillon

 

·      Densité de probabilité

La rentabilité d’un actif mesure la variation en pourcentage de sa valeur au cours d’une période donnée. Par définition, la rentabilité future d’un actif risqué est inconnue ex-ante, mais il est possible de définir plusieurs états de la nature qui correspondent à différents niveaux de rentabilité et d’associer à chacun de ces états une probabilité de réalisation. Ces informations peuvent être représentées à l’aide d’une densité de probabilité, qui associe une probabilité P_R à chaque rentabilité possible R.

Prenons un exemple. L’action BFI cote actuellement 100 €. Les analystes prévoient que le prix de cette action sera de 140 € dans un an avec une probabilité de 25 %, de 110 € avec une probabilité de 50 % et de 80 € avec une probabilité de 25 %. L’entreprise BFI ne verse pas de dividendes. Le tableau suivant donne     la densité de probabilité des rentabilités de l’action BFI :

 

 

Les rentabilités de l’action BFI l’année prochaine seront donc respectivement de 40 %, 10 % et – 20 % dans les trois états de la nature possibles. Il est également possible de représenter cette densité à l’aide d’un histogramme.

         

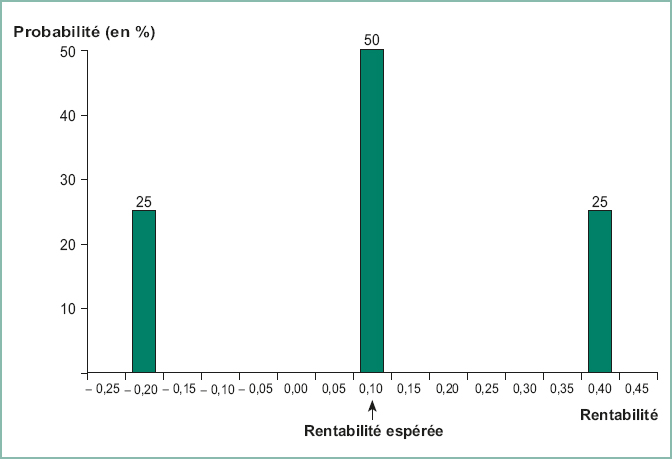
Histogramme de la densité de probabilité des rentabilités de l’action BFI

 

La hauteur de chaque barre mesure la probabilité d’observer la rentabilité indiquée en abscisse.

 

·      Rentabilité espérée

À partir de cette densité de probabilité, il est possible de calculer la rentabilité espérée. Celle-ci est égale à la moyenne des rentabilités possibles, chaque rentabilité étant pondérée par sa probabilité d’occurrence :

La rentabilité espérée est celle qu’un investisseur obtiendrait en moyenne s’il pouvait effectuer le même investissement un grand nombre de fois (les rentabilités provenant à chaque fois de la même densité de probabilité). Dans l’histogramme précédent, la rentabilité espérée est le point d’équilibre de la densité (si l’on considère les probabilités comme des pondérations). Pour l’action BFI, la rentabilité espérée est donc :

·      Rentabilité historique

La rentabilité effective, ou historique, ou constatée, est la rentabilité qui a effectivement été réalisée par un actif donné au cours d’une période définie et passée. Comment la calculer ? Prenons l’exemple d’une action. Cette action a un prix P_t à la date t. En date t + 1, si cette action verse un dividende Div_t+1 et que son prix est P_t+1, la rentabilité effective de la détention de cette action entre les dates t et t + 1 est :

  

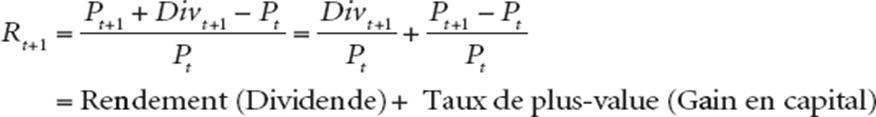
La rentabilité effective R_t+1 entre les dates t et t + 1 correspond donc à la somme du dividende et du gain en capital, exprimés en pourcentage du prix initial de l’action. Si l’action est détenue au-delà du premier dividende, la mesure de la rentabilité effective nécessite de poser une hypothèse relative à la façon dont seront traités les dividendes futurs : seront-ils immédiatement réinvestis pour acheter des actions supplémentaires ou seront-ils utilisés à autre chose ? Lorsqu’on cherche à mesurer la rentabilité effective d’un actif donné, la logique veut que les dividendes soient réinvestis. On peut par conséquent recourir à l’équation ci-dessous pour calculer la rentabilité de l’action entre chaque versement de dividende.

Ces rentabilités effectives peuvent ensuite être composées pour calculer la rentabilité effective sur un horizon plus long. Ainsi, si l’action verse un dividende à la fin de chaque année, les rentabilités annuelles R1,…, R4 et la rentabilité effective sur quatre ans R_1–4 sont telles que :

Par exemple, le prix de l’action Total, ainsi que la valeur et la date de versement des dividendes sont présentés dans le tableau suivant :

  

       

 

Quelle a été la rentabilité effective de l’action Total en 2019 ?

 

Entre le 1er janvier et le 19 mars, la rentabilité de l’action Total est égale à :

La rentabilité sur l’année de l’action Total est :

Cette application rappelle que la rentabilité d’un actif provient à la fois des flux auxquels il donne droit (les dividendes dans le cas d’une action) et des gains en capital. Oublier l’une de ces deux composantes conduit à une vision erronée de la performance. Les rentabilités de n’importe quel actif financier se calculent suivant la même logique. Celle d’un portefeuille se calcule simplement en tenant compte de tous les flux reçus et de la valeur de marché du portefeuille à chaque date d’occurrence d’un flux.

Avec Rt la rentabilité effective d’un titre en année t, la rentabilité annuelle moyenne entre l’année 1 et l’année T du titre peut être calculée avec la formule suivante :

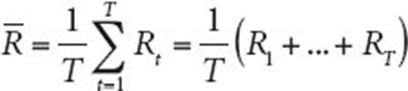
La rentabilité annuelle moyenne d’un titre est le point central de la densité de probabilité empirique de ses rentabilités annuelles. Sous l’hypothèse de stabilité de la densité de probabilité, la rentabilité annuelle moyenne d’un actif constitue une estimation de sa rentabilité espérée.

·      Variance et Ecart-type

La variance et l’écart-type sont les deux mesures les plus courantes du risque. La variance, notée σ², est l’espérance du carré des écarts à la moyenne. L’écart-type, σ, est simplement la racine carrée de la variance :

                                                                                                                   

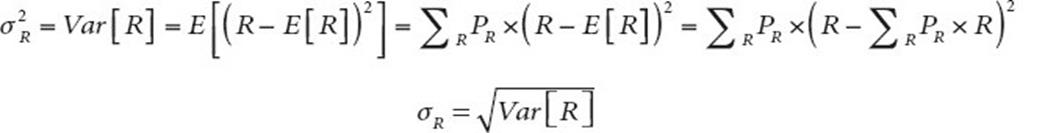
     La variance représente une mesure de dispersion autour de la moyenne (espérance) de la densité des rentabilités. Dans le cas de l’action BFI, la variance est :

L’écart-type des rentabilités de l’action BFI est donc :   

    

     L’écart-type des rentabilités est fréquemment appelé la volatilité. Bien que la variance et l’écart-type mesurent tous deux la volatilité des rentabilités d’un actif, il est plus simple d’utiliser l’écart-type car il s’exprime dans la même unité de mesure que les rentabilités.

Variance et volatilité des rentabilités

On peut également estimer la variance à partir des rentabilités effectives grâce à la formule :

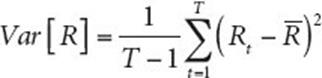
Exemple : A partir des données du tableau suivant, quelles sont la variance et la volatilité des rentabilités du CAC40 sur période 2001-2009 ?

La rentabilité annuelle moyenne du CAC 40 sur cette période est de 5,6 %. La variance est :

La volatilité (écart-type) des rentabilités du CAC 40 sur la période est 

 

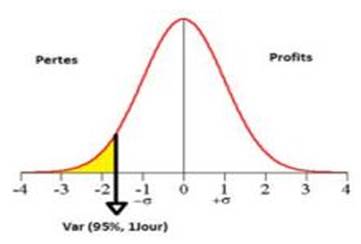
·       Value at Risk (VaR)

 

La « Value at Risk » ou valeur en risque  d’un portefeuille pour la durée et le niveau de probabilité c se définit comme le montant tel que la perte encourue sur ce portefeuille pendant la durée de 0 à t ne dépassera la « Value at Risk » qu’avec une probabilité de 1-c.

 On peut donc écrire :

P (perte > VaR) = 1-c

                    P (perte <= VaR) = c

La « Value at Risk » d’un portefeuille est donc la perte la pire attendue sur un horizon de temps donné (généralement 1 an ou moins) pour un niveau de confiance donné (95 ou 99%). La VAR au seuil de confiance de 95 % à 1 jour, égale à 1 million d’euros, signifie qu’il y a 95 % de chances pour que la perte associée à la détention de l’actif n’excède pas 1 million.

 

 

Les principales méthodes de calcul de la VaR peuvent être classées en trois catégories : la simulation historique, la méthode analytique ou paramétrique, la méthode de simulation de Monte Carlo.

-        La simulation historique

La méthode de simulation historique ou méthode historique, est la méthode la plus simple puisqu’elle ne fait aucune hypothèse sur la forme de la distribution des rentabilités. Il suffit en fait de disposer des données historiques des gains et des pertes journalières du portefeuille dont on souhaite calculer la VaR.

On constitue une distribution empirique des gains et des pertes journaliers. Il s’agit donc de choisir une période d’observation (ou fenêtre) qui peut varier de 6 mois à 4 ans voire plus (dans le cas des banques). Les rendements dans cette fenêtre sont rangés par ordre croissant. Selon le niveau de confiance « c » et le nombre journalier d’observations « n ». On calcule la VAR à 1 jour qui doit se trouver à : n x (1-c).

Exemple: Soit un portefeuille composé de plusieurs actifs. Afin de calculer la VaR historique à un jour sur ce portefeuille il faut relever l'ensemble des gains et des pertes quotidiennes réalisées sur les 1 000 derniers jours (par exemple). Une fois toutes ces données obtenues, il faut les classer par ordre croissant. Si l'on souhaite obtenir la VAR à 99%, il suffira de trouver la 10ème (1000*(100%-99%)) valeur obtenue.

La VaR est alors définie comme un quantile de la distribution empirique des profits/pertes futurs selon le niveau de confiance choisi α%.

Un autre Exemple de calcul de VaR historique:

100 rendements quotidiens ont été collectés sur un portefeuille de 100 millions d’euros. Après les avoir classés par ordre décroissant, voici les 5 plus petits rendements journaliers :

-0.0101 ; -0.0097 ; -0.0043 ; -0.0038 ; -0.0018

La VaR à 5% correspondra à la 5ème plus petite observation soit -0.18%.

Ainsi on pourra conclure que le portefeuille à 5% de chances de réaliser une perte supérieure à 180 000 euros sur une journée (0.0018 * 100 000 000 = 180 0000).

 

 

-        La méthode paramétrique ou méthode variance-Covariance

La méthode paramétrique, développée par JP Morgan via RiskMetrics, suppose que les rentabilités des facteurs de risque suivent une loi normale multivariée avec des corrélations stables et une sensibilité constante. La matrice de variance-covariance est estimée à partir d'observations passées, permettant un calcul analytique de la VaR grâce à l'hypothèse de normalité et de linéarité.

A partir de la loi normale inversée, on calcule le coefficient qui correspond à l’écart maximum attendu pour une VAR du niveau de confiance choisi sur une durée déterminée.

Par exemple, si l’on considère un niveau de confiance de 99 % et une VAR à un jour, l’écart maximum, calculé à partir de la loi normale inversé est égal à 2,3263. Pour une VAR à n jours, on multiplie par √n. Si l’on considère maintenant un portefeuille composé de titre A de 1000 000 euros, avec une volatilité annuelle de 20 %, pour calculer la VaR à 99 % pour 1 jour, il faut connaitre la volatilité journalière du portefeuille (en France, on considère l’année de 252 jours ouvrables).

 

Le fait d’investir dans un autre portefeuille B, sur lequel on peut également calculer la VAR, va, tout comme dans la gestion d’un portefeuille, permettre de modifier la VAR du nouveau portefeuille constitué. Il faut en effet tenir compte de la corrélation entre les deux portefeuilles. La formule à appliquer est alors :

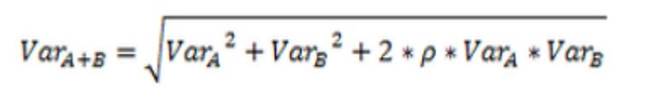
Où ρ représente le coefficient de corrélation.

 

-        La méthode Monte Carlo

La méthode de simulation de Monte Carlo utilise un modèle économétrique pour déterminer l’évolution des facteurs de risque au cours du temps. Cette méthode de simulation repose sur une multitude de scénarii aléatoires définis à partir du modèle économétrique.

Par exemple, Un opérateur souhaite investir sur une action aujourd'hui et la revendre dans un an (espérant ainsi la revendre plus cher qu'il ne l'a acheté). Mais durant ce laps de temps, l'action est soumise à des fluctuations. L'opérateur souhaitant ainsi déterminer la VAR de cette action va simuler par Monte Carlo, 10 000 variations possibles (par exemple), puis calculer les pertes ou les gains réalisés dans chacune de ces simulations.

Si l'opérateur souhaite obtenir une VAR à 99%, il lui suffira de repérer la 100ème pire perte afin de pouvoir affirmer avec 99% de chances que la perte qu'il réalisera sur cette opération ne dépassera pas ce montant.

-        Limites et défis de la VaR 

La Value at Risk (VaR) est une mesure largement utilisée de la perte potentielle d’un portefeuille d’actifs sur une période donnée et un niveau de confiance donné. Cependant, la VaR n’est pas une mesure parfaite et elle présente certaines limites et critiques :

 

► La VaR n'est pas une mesure de risque cohérente. Elle ne respecte pas les propriétés de subadditivité et d'homogénéité positive. Cela peut entraîner des évaluations de risque trompeuses, surtout pour des portefeuilles complexes. En revanche, l'Expected Shortfall (ES) est une mesure cohérente qui évalue mieux le risque extrême en calculant la perte moyenne au-delà de la VaR.

►  La VaR est sensible au choix des paramètres et des hypothèses.  Comme l'horizon temporel et le niveau de confiance, ce qui peut entraîner des estimations très différentes. Par exemple, un horizon plus long ou un niveau de confiance élevé augmente la VaR, tandis qu'une distribution normale peut sous-estimer le risque. Pour surmonter ces défis, des backtests et des stress tests peuvent être utilisés pour valider et ajuster les estimations de la VaR.

► La VaR ne fournit pas d'informations sur l'ampleur et la fréquence des pertes au-delà du niveau de la VaR.  La VaR indique la perte maximale attendue avec une certaine probabilité sur une période donnée, mais ne renseigne pas sur les pertes plus importantes ou sur des périodes plus longues. Par exemple, une VaR de 10 millions de dollars à 95 % signifie qu'on peut perdre plus de 10 millions seulement 5 % du temps, sans préciser l'ampleur des pertes extrêmes. Cela peut engendrer un faux sentiment de sécurité et exposer le portefeuille à des risques non pris en compte.

Une façon possible de résoudre ce problème consiste à utiliser des mesures de risque complémentaires telles que l'ES, des mesures de risque extrême telles que la Valeur conditionnelle à risque (CVaR) ou la Tail Value at Risk (TVaR), et des indicateurs de risque tels que l'asymétrie et l'kurtosis pour compléter les informations fournies. Ces mesures complémentaires seront étudiées en EME II.

 RISQUE ET RENDEMENT D’UN PORTEFEUILLE

·      Diversification de portefeuille

La diversification de portefeuille est une stratégie d’investissement basique qui consiste à créer un portefeuille d’actifs différents dans l’objectif de diminuer le risque lié au portefeuille. La diversification réduit l'exposition au risque en combinant des actifs aux variations de prix non corrélées. Lorsqu’un portefeuille contient différentes actions, les risques spécifiques liés à chaque action vont se compenser grâce à la diversification : des bonnes nouvelles feront augmenter certaines actions contenues dans le portefeuille tandis que des mauvaises nouvelles en feront baisser d’autres. En moyenne, les variations des prix des actions provoquées par les informations spécifiques se compenseront entre elles. Par exemple, posséder deux actifs permet de limiter la perte à 5 % si l'un perd 10 %. Cependant, chaque ajout d'actifs entraîne des coûts de transaction, rendant l'optimisation délicate, avec un nombre idéal d'environ 25 actifs. Le risque systémique, lié à des événements exogènes ou à la conjoncture économique, reste non diversifiable. L'essor des ETF (Exchange- traded Funds), qui suivent des indices comme le S&P 500 ou le Nasdaq, augmente la corrélation entre actions, bien que cette affirmation nécessite encore des preuves académiques.

Le choix de la diversification sectorielle et géographique a principalement du sens pour éviter d’investir dans des actions corrélées entre elles.  La corrélation de deux actions signifie que la baisse de l’une se traduit par la baisse de l’autre et réciproquement. Autrement dit, elles suivent plus ou moins les mêmes fluctuations de marché. Dès lors, pour vérifier votre niveau de diversification, il apparaît important de mesurer l’indice de corrélation de votre portefeuille.

Exemple de portefeuille diversifié 

Pour illustrer concrètement la diversification d'un portefeuille, prenons l'exemple d'un investisseur fictif nommé Paul. Il souhaite construire un portefeuille diversifié pour minimiser ses risques tout en cherchant à maximiser ses rendements sur le long terme. Voici comment Paul pourrait structurer son portefeuille :

Classe d'actifs	Pourcentage du portefeuille	Niveau de risque	Description	Enveloppes recommandées
Actions internationales	30%	Élevé	Investissements dans des entreprises situées hors du pays de résidence, visant la croissance mondiale.	Assurance vie ou compte titres
Actions nationales	25%	Modéré à élevé	Investissements dans des entreprises basées dans le pays de résidence, pour capter la croissance locale.	PEA ou Assurance vie
Obligations d'État	20%	Faible à modéré	Obligations gouvernementales offrant une sécurité relative mais des rendements plus faibles.	Assurance vie ou compte titres
Fonds immobiliers	10%	Modéré	Immobilier comme classe d'actif tangible offrant des revenus locatifs et une possible appréciation.	Assurance vie ou compte titres
Crypto monnaies	5%	Très élevé	Capter la performance spéculative de cette classe d'actif	Cold wallet
Fonds indiciels écologiques (ETF)	5%	Modéré	Fonds se concentrant sur des entreprises écoresponsables, combinant éthique et rendement.	Assurance vie Goodvest
Liquidités et équivalents	5%	Très faible	Liquidités pour couvrir les dépenses imprévues et saisir les opportunités d'investissement.	Livrets bancaires

 

Ce tableau montre une répartition équilibrée entre différentes classes d'actifs, chacune comportant ses propres niveaux de risque et de rendement.

 

NB : la diversification du portefeuille réduit sa volatilité, mais elle ne peut pas annuler le risque car seul le risque spécifique disparaît avec l’augmentation de la taille du portefeuille. Le risque systématique du portefeuille, lui, demeure indépendant de sa taille.

 

 

Observation : l’illusion de la diversification temporelle

La diversification temporelle, qui consiste à croire qu'un investissement à long terme réduit le risque, est fallacieuse. Bien que la volatilité de la rentabilité annuelle moyenne diminue avec le temps, la volatilité de la rentabilité cumulée augmente. Une baisse initiale significative peut avoir un impact durable sur la valeur finale du portefeuille, comme observé lors de la crise financière de 2008. La théorie du retour vers la moyenne n'est pas prouvée sur des périodes courtes, et une stratégie d'achat-détention n'est pas optimale. Il serait plus judicieux d'acheter après des périodes de faibles rendements et de vendre après des périodes de rendements élevés.

 

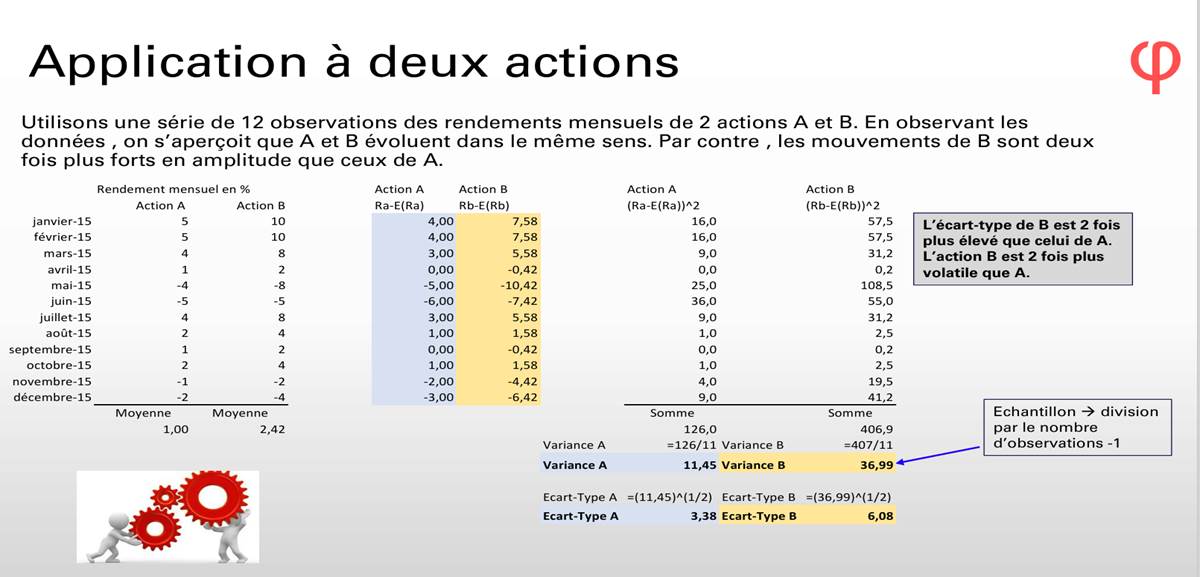
·      Rendement d’un portefeuille d’Actifs

C’est la moyenne pondérée du rendement des valeurs qui constituent le portefeuille. La pondération de chaque valeur est égale au pourcentage investi dans la valeur par rapport à la totalité investie dans le portefeuille.

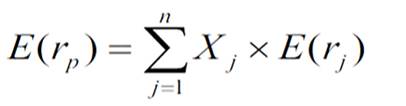
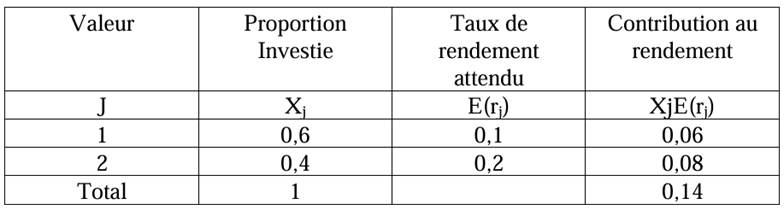
Exemple : Le tableau ci-dessous décrit un portefeuille constitué de deux valeurs distinctes et permet de calculer le rendement attendu du portefeuille à partir du rendement attendu de chaque valeur, et de son poids dans le portefeuille.

 

·       Risque d’un portefeuille

Le risque du portefeuille n'est pas la moyenne pondérée des risques des titres qui le composent. En effet, les variations de rendement de deux titres peuvent se compenser (au moins partiellement) lorsqu'elles sont de sens opposé. Le risque du portefeuille dépend donc de la covariance des titres qui le composent.

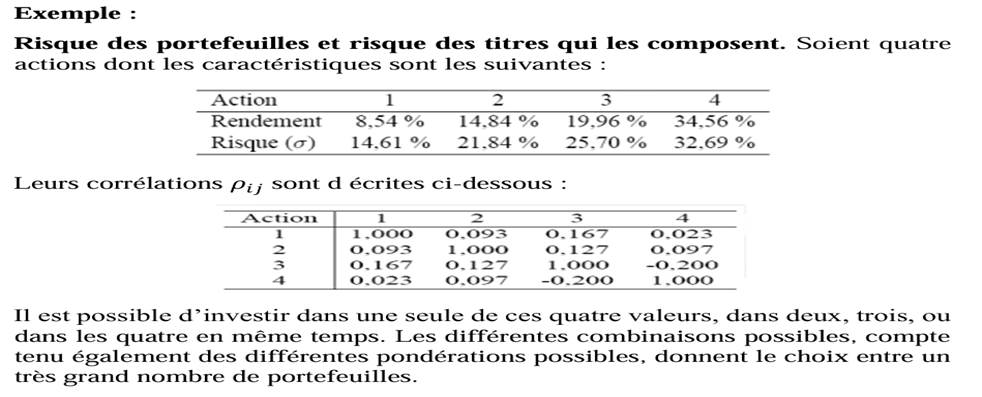
Si le vieil adage "ne pas mettre tous ses œufs dans le même panier "était appliqué depuis longtemps par les praticiens, Markowitz (1952) fut le premier, avec Roy (1952), à formaliser mathématiquement le principe de diversification des risques.

 

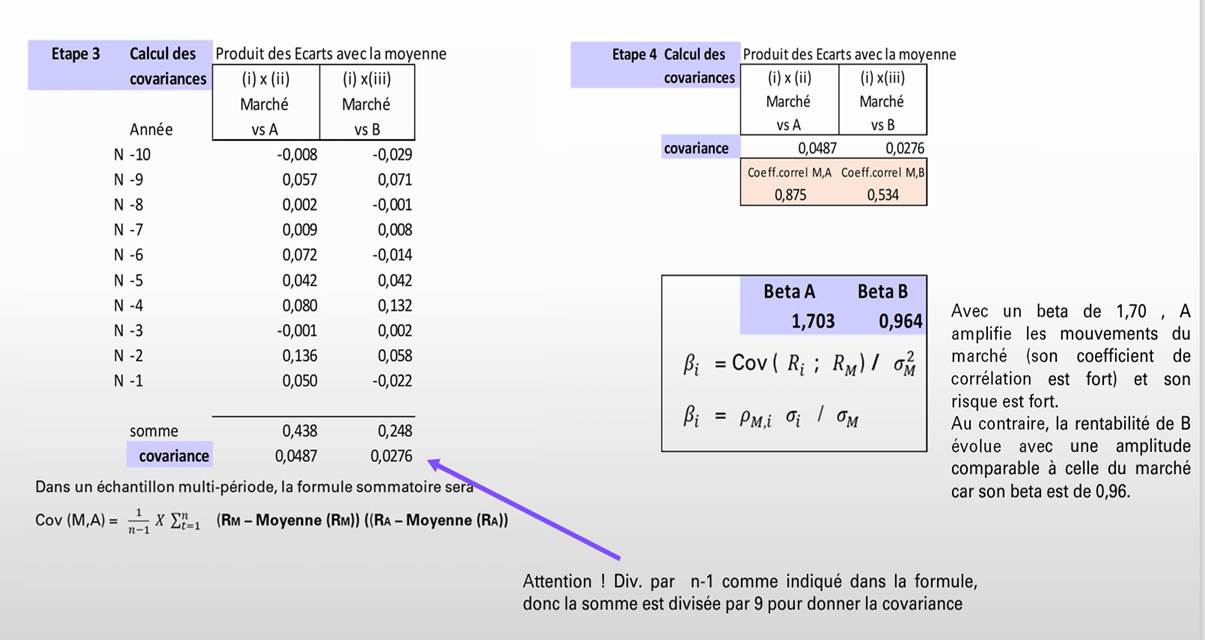
-        Covariance

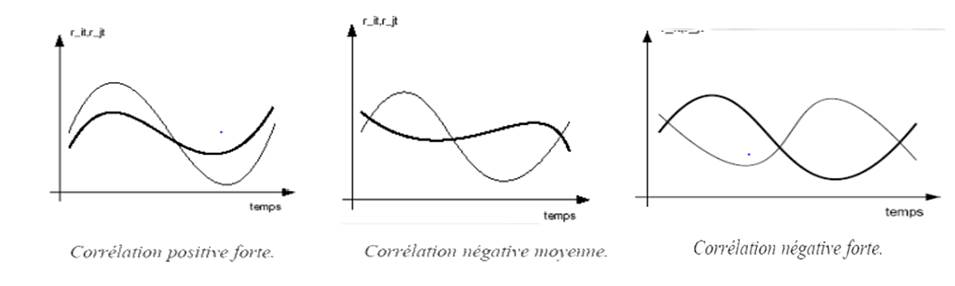
Soit deux actions, i et j, dont le rendement moyen observé est respectivement Ri et Rj. La covariance entre les deux va tenir compte des similitudes (covariance élevée) ou des différences (covariance faible) dans l’évolution des rendements observés, respectivement Rit et Rjt, par rapport à leur moyenne. Et cela par confrontation, pour chaque date t, de l’amplitude et du signe des écarts.

(Rit – Ṝi) et (Rjt – Ṝj)

La covariance peut alors être perçue comme une moyenne du produit de ces écarts.

 

-        Corrélation

La corrélation mesure le degré et le sens de la relation qu’ont en commun deux variables, ici le rendement de deux actifs risqués. Son calcul nécessite avant tout celui d’une covariance qui contribue également à évaluer la nature de cette relation. Il est cependant difficile d’interpréter et de comparer la valeur des covariances, en dehors de leur signe, puisqu’on ne dispose pas d’échelle de mesure dans l’absolu. La corrélation pallie ce problème en transposant la covariance dans l’intervalle [-1 ; +1]. Le coefficient de corrélation entre i et j, noté ρ ij apporte donc le complément d’information nécessaire, par le rapport de la covariance aux écarts-type de chacune des deux actions :

 

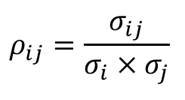
La mesure de la variance du rendement du portefeuille dans le cas de deux valeurs :

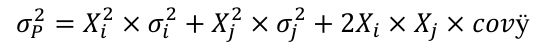
Exemple :

Soit un portefeuille constitué de deux valeurs A et B aux caractéristiques suivantes :

E(rA ) = 10 %      sA = 12 %                    

E(rB ) = 8 %        sB = 15 %                   

covA,B = -0,0144

Calculer le rendement et le risque d'un portefeuille composé de 60% de A et 40% de B ?

Rendement du portefeuille : E (rp) = (60% × 10%) + (40% × 8%)

                                                           = 9.2%

Risque du portefeuille  = 0,62 × 0,122 × 0,4 × 0,152 + 2 × 0,6 × 0,4 × (-0,0144)

                                               = 0,001872

                                            

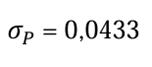
Le risque d'un portefeuille de n valeurs est donné par la relation.

 

 

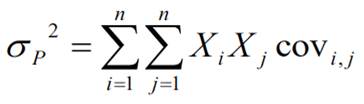
·       Mesure du risque systématique

Le risque systématique est le risque qui affecte l'ensemble du marché, plutôt qu'une entreprise ou un secteur spécifique. Il est également connu sous le nom de risque de marché, risque non diversifiable ou risque de volatilité.

Lorsqu’un investisseur évalue le risque d’un investissement (et donc la prime de risque requise), il ne considère que le risque systématique, impossible à éliminer par la diversification.

-        Identifier le risque systématique : le portefeuille de marché

La mesure du risque systématique d'un actif nécessite d'évaluer sa sensibilité aux chocs systématiques qui influencent l’économie dans son ensemble, en observant comment sa rentabilité varie avec celle d'un portefeuille exposé au risque de marché. Il faut pour ce faire trouver un portefeuille qui soit exclusivement exposé au risque systématique, c’est-à-dire un portefeuille dont les variations de sa rentabilité ne seront liées qu’aux chocs systématiques subis par l’économie. Un tel portefeuille, est un portefeuille efficient. L’identification d’un portefeuille efficient est l’une des questions centrales de la finance moderne.

Un portefeuille efficient, complètement diversifié, contient un grand nombre d'actifs et ne permet plus de réduire le risque sans diminuer la rentabilité espérée. L'approche maximale de diversification est le portefeuille de marché, souvent approximé par des indices boursiers larges comme le CAC All-Tradable ou le S&P 500. Cette simplification repose sur l'hypothèse que ces indices sont suffisamment diversifiés pour représenter le risque systématique.

 

 

-        Sensibilité au risque systématique : le bêta

Sous l’hypothèse que le portefeuille de marché (ou le CAC 40 par exemple) est efficient, sa rentabilité ne dépend que des chocs systématiques affectant l’économie. Il est alors possible de mesurer le risque systématique d’un titre en calculant la sensibilité de sa rentabilité aux modifications de la rentabilité du portefeuille de marché. Cela consiste à calculer son bêta :

Le bêta β d’un actif représente la variation espérée, en pourcentage, de sa rentabilité suite à une modification de 1 % de celle du portefeuille de marché.

 

Application (Estimation du bêta) 

La rentabilité du portefeuille de marché augmente de 47 % lorsque l’économie est en croissance et baisse de 25 % en période de récession. Quel est le bêta d’une action de type S dont les rentabilités sont respectivement de 40 % et – 20 % dans ces deux états de la nature ? Quel est le bêta d’une action de type I ?

Solution

Le risque systématique lié à la conjoncture économique fait varier la rentabilité du portefeuille de marché de 47 % – (– 25 %) = 72 %.

La rentabilité d’une action de type S se modifie, elle, de 40 % – (– 20 %) = 60 %.

Le bêta d’une action S vaut donc :

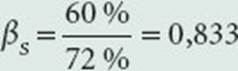
Une modification de 1 % de la rentabilité du portefeuille de marché correspond en moyenne à une variation de 0,833 % de la rentabilité d’une action S.

Ne pas confondre le bêta et la volatilité

La volatilité mesure le risque total d'un actif (risque systématique et risque spécifique), tandis que le bêta évalue uniquement le risque systématique. Par exemple, Airbus et Atos présentent des volatilités proches (35 à 40 %), mais des bêtas différents (1,15 pour Airbus et 1,44 pour Atos). Les risques totaux des deux titres sont proches, mais Atos a une plus grande exposition au risque systématique, en raison de sa spécialisation, tandis qu'Airbus, avec ses activités diversifiées (aéronautique, défense, espace), est moins sensible aux fluctuations économiques.

·       Modèle d’évaluation des actifs financiers (MEDAF)

Le MEDAF est le résultat de la liaison rendement-risque. C’est donc la relation entre rentabilité attendue et risque de titres et de portefeuilles. IL postule que le taux de rentabilité exigé par un investisseur sur un titre i est lié au risque de marché.

Hypothèses du modèle :

 

Les investisseurs ont de l'aversion pour le risque ;

 Ils ont le même horizon de prévision et formulent les mêmes anticipations ;

Les taux de prêt et d'emprunt sont les mêmes ;

 Il n'existe ni impôt ni coûts de transaction ;

Les investisseurs sont rationnels et cherchent à détenir des portefeuilles efficaces au sens de Markowitz.

 

 

Le βi est une mesure du risque du titre i en unités de risque de marché. Il indique la volatilité relative du rendement de la valeur par rapport au rendement du marché.

Un β > 1 indique donc une valeur plus risquée que le marché (qui amplifiera les  variations du marché).

Inversement, une valeur au β < 1 variera dans des proportions plus faibles que le marché.

 

     Le coefficient bêta est égal à la covariance du rendement du titre par rapport au rendement du marché sur la variance du rendement du marché :

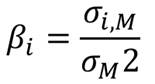
Dans le cas d'un portefeuille, le bêta est une combinaison linéaire du bêta des différentes valeurs qui le composent. Le bêta d’un portefeuille est la moyenne des bêtas des titres qui le composent, pondérée par le poids de ces titres dans le portefeuille.

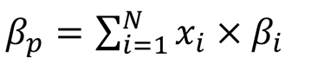
Son utilisation dans le MEDAF permet de déterminer facilement le rendement espéré du portefeuille compte tenu de ce risque.

 

 

-       Exemple d’application sur le MEDAF et le calcul du Bêta

 

 

 

 

-       Comment calculer le Bêta ?

 

 

 

 

 

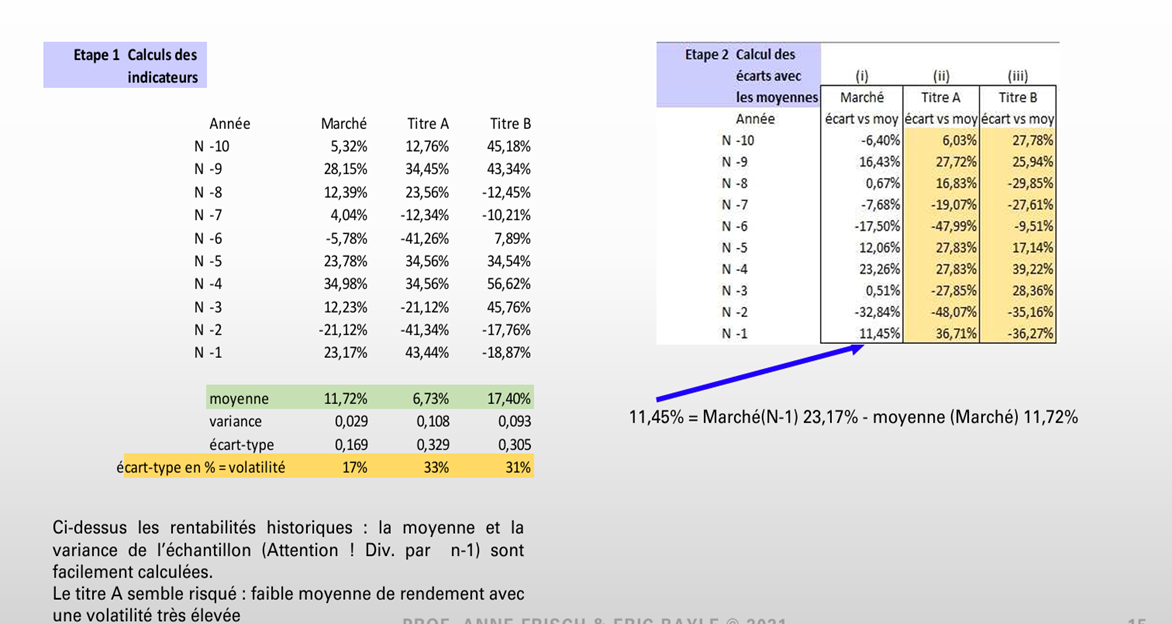
Bêta du Portefeuille exemple

 

 

 

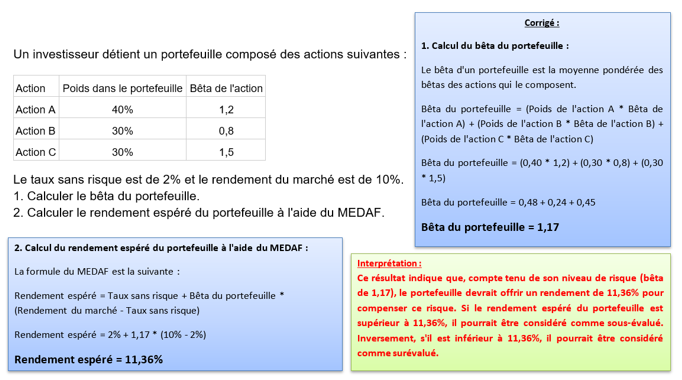
-       Pour conclure sur le MEDAF

 

 

RENDEMENT ET PERFORMANCE

 

Dans le domaine de la finance, l'évaluation du rendement et de la performance des investissements est essentielle pour les investisseurs. Cette évaluation repose sur des mesures ajustées au risque, permettant de comparer efficacement différents actifs et d'optimiser les portefeuilles en fonction des objectifs financiers.

·       Mesures de Performance ajustées au risque

Lorsqu’il faut gérer le portefeuille, comprendre les rendements ajustés au risque est crucial pour les investisseurs qui cherchent à équilibrer risque et rendement dans un marché volatil. Deux mesures largement utilisées pour évaluer les rendements ajustés au risque sont le ratio de Sharpe et le ratio de Sortino. Ces ratios fournissent des informations précieuses sur la performance des portefeuilles d'investissement et aident les investisseurs à prendre des décisions éclairées.

-        Le Ratio de SHARPE

Du nom du lauréat du prix Nobel William F. Sharpe, le ratio de Sharpe est défini comme le rapport entre le rendement excédentaire d'un investissement (ou d’un portefeuille) et la volatilité de ce placement (ou de ce portefeuille), c’est-à-dire l'écart-type de ses rendements. Le rendement excédentaire est le rendement d’un investissement au-delà du taux sans risque. En d'autres termes, le ratio de Sharpe mesure combien de rendement additionnel un investisseur peut espérer pour chaque unité de risque assumée.

 

 

Voici la formule mathématique du ratio de Sharpe : (Rp - Rf) / σp    Où

• R_p représente le rendement du portefeuille,
• R_f est le taux de rendement sans risque, souvent basé sur le rendement des obligations d'État,
• σ_p représente l'écart-type des rendements du portefeuille, une mesure de sa volatilité.

 

Les ratios de Sharpe sont souvent utilisés pour déterminer la performance relative des portefeuilles, des traders et des gestionnaires de fonds dans le temps. Les ratios de Sharpe des différentes classes d'actifs se situent généralement aux alentours de 0,2 à 0,3 sur le long terme.

Une valeur comprise entre 0 et 1 signifie que les rendements obtenus sont meilleurs que le taux sans risque, mais que leur excès de risque dépasse leur excès de rendement.

Une valeur supérieure à 1 indique que les rendements sont non seulement meilleurs que le taux sans risque, mais que les rendements excédentaires sont supérieurs à leurs risques excédentaires.

Un ratio de Sharpe négatif signifie que la performance d'un gestionnaire ou d'un portefeuille est inférieure au taux sans risque. Pour les actifs financiers, les ratios de Sharpe négatifs ne persistent pas pendant des périodes indéfinies. Les économies capitalistes cesseraient de fonctionner si cela était vrai.

Exemples et mesures

Pour illustrer l'utilisation pratique du ratio de Sharpe, considérons deux portefeuilles hypothétiques:

Portefeuille A:

- Rendement : 10%

- Taux sans risque : 2%

- Ecart-type : 8%

Ratio de Sharpe = (10% - 2%) / 8% = 1,0

Portefeuille B:

- Rendement : 15%

- Taux sans risque : 2%

- Ecart-type : 15 %

Ratio de Sharpe = (15 % - 2 %) / 15 % = 0,86

Bien que le portefeuille B ait un rendement plus élevé, son risque plus élevé (écart-type) réduit sa performance ajustée au risque. Le ratio de Sharpe du portefeuille B de 0,86 indique un rendement ajusté au risque plus faible que celui du portefeuille A, qui est de 1,0. En comparant les rendements excédentaires à la volatilité de ces rendements, les investisseurs peuvent prendre des décisions plus éclairées.

Avantages :

• Simplicité d'application : Facile à utiliser sur n'importe quelle série chronologique de rendements.
• Comparabilité : Permet de comparer différents investissements en termes de rendement ajusté au risque.

• Mesure ex-post : Utilisé pour évaluer les performances passées, offrant une vue d'ensemble de la rentabilité.

Inconvénients :

• Volatilité comme seul indicateur : Considère toute volatilité comme nuisible, ne distinguant pas entre volatilité positive et négative.
• Hypothèses de normalité : Suppose que la distribution des rendements est normale, ce qui n'est souvent pas le cas dans la réalité.
• Sensibilité aux performances passées : Les résultats peuvent être biaisés car les performances passées ne prédisent pas nécessairement les résultats futurs.
• Absence d'unité de mesure : Exprimé sous forme de nombre sans lien direct avec des pourcentages ou des rendements, ce qui limite son interprétation.

Le ratio de Sharpe est un outil pertinent pour évaluer la performance financière d’un placement en tenant compte du risque associé à cet investissement. Il peut se calculer pour un placement spécifique ou pour un portefeuille d'investissement. Pour les investisseurs, ce ratio permet d'effectuer des comparaisons entre différents investissements, d'optimiser la composition de leur portefeuille, et de mieux gérer les risques à leurs investissements. 

Pour pallier certaines de ces limites, d'autres ratios tels que le ratio de Sortino (qui ne prend en compte que la volatilité à la baisse) peuvent être utilisés pour une analyse plus fine du risque.

 

-        Le Ratio de SORTINO

Le ratio de Sortino est une mesure importante dans l'analyse des investissements, en particulier pour ceux qui se concentrent sur la minimisation du risque de baisse. En faisant la distinction entre la volatilité nuisible (risque de baisse) et la volatilité globale, le ratio de Sortino offre une vision plus nuancée de la performance d'un portefeuille. Il est très similaire au ratio de Sharpe, mais le ratio de Sortino est conçu pour améliorer le ratio de Sharpe en faisant la distinction entre la volatilité à la hausse et à la baisse. Alors que le ratio de Sharpe pénalise également la volatilité à la hausse et à la baisse, le ratio de Sortino ne pénalise que la volatilité à la baisse.

Calcul du ratio de Sortino

Le ratio de Sortino, S, est défini comme suit :

S = (R - T) / DR

Où :

• R = Rendement moyen réalisé du portefeuille ou de la stratégie
• T = Taux de rendement requis
• DR = Ecart à la baisse cible / "risque à la baisse".

DR est égal à :

DR = √ [ ∫ (T - r)² * f(r).dr ]

Où :

• T = Comme ci-dessus, le taux de rendement requis.
• r = Rendement de la distribution des rendements annuels, f(r).
• f(r) = Distribution de probabilité des rendements annuel.

La fonction de calcul intégral est prise sur la zone T à -∞ (infini négatif). Une fonction continue, plutôt que discrète, est utilisée pour éviter d'avoir besoin de rendements mensuels pour avoir suffisamment de points de données pour effectuer un calcul statistiquement précis. Cela signifie que l'objectif de rendement annuel doit être calculé en termes mensuels, ce qui a des implications pour l'identification des risques. Par exemple, si l'on exige un rendement de 10 % par an, l'exigence d'un rendement de 0,8 % par mois permettra d'identifier un risque plus élevé que l'objectif annuel.

Avantages :

• Prise en compte de l'asymétrie : Récompense les portefeuilles avec une asymétrie positive, valorisant davantage les hausses que les baisses.
• Focus sur le risque de baisse : Pénalise uniquement les rendements en dessous d'un seuil cible, ce qui est plus pertinent pour la gestion des risques.
• Évaluation plus précise : Mieux adapté pour les stratégies qui présentent des rendements positifs réguliers avec des baisses sporadiques et significatives.

 

Inconvénients :

• Complexité relative : Peut-être moins intuitif à utiliser que le ratio de Sharpe pour certains investisseurs.
• Dépendance au seuil cible : La détermination du taux de rendement cible peut influencer les résultats, rendant l'interprétation plus subjective.
• Limitation face à l'asymétrie négative : Pénalise les stratégies avec des rendements faibles mais des pertes importantes, ce qui peut ne pas convenir à tous les types d'investissements.

Exemple de calcul du ratio de Sortino

Disons que nous avons l'ensemble suivant de rendements annuels :

10%, 4%, 15%, -5%, 20%, -2%, 8%, -6%, 13%, et 23%.

-        Première étape

Le rendement annuel moyen est la somme de ceux-ci (80 %) divisée par le nombre de rendements (dix), soit 8 %. Disons que le rendement cible est le rendement annualisé attendu du S&P 500, soit environ 7 %.

Par conséquent, le rendement excédentaire est de 1 % soit  (8 % - 7 %).

-        Deuxième étape

Ensuite, nous calculons l'écart à la baisse. Nous prenons en compte les valeurs négatives, qui sont -5%, -2%, et -6%. Les écarts à la baisse des autres sont nuls, étant donné qu'il s'agissait de rendements positifs.

 

-        Troisième étape

On élève ces valeurs au carré :  -5%^2 = 0.0025 ;  -2%^2 = 0.0004 ;  -6%^2 = 0.0036

La moyenne de ces écarts à la baisse est la somme divisée par le nombre de retours (10) :

 

0.0025 + 0.0004 + 0.0036 = 0.0065 et 0.0065 / 10 = 0.00065 = 0.065%

-        Quatrième étape

Ensuite, il faut calculer l'écart à la baisse cible. Il s'agit de la racine carrée de la réponse de l'étape 3 :

√0.00065 = 0.0255

-        Cinquième étape

Enfin, calculez le ratio de Sortino, en prenant le rendement excédentaire de la première étape et en le divisant par l'écart à la baisse cible de la quatrième étape.

0.01 / 0.0255 = 0.392        S= 0.392

Étant donné que la plupart des catégories d'actifs produisent des ratios de Sortino d'environ 0,2 à 0,3 sur le long terme, il s'agit d'un ratio raisonnable.

·       Optimisation de portefeuille

L'optimisation de portefeuille vise à maximiser les rendements espérés tout en minimisant le risque, en identifiant la combinaison optimale d'actifs. La frontière efficiente représente l'ensemble des portefeuilles offrant le meilleur rendement pour un niveau de risque donné.

-        Rentabilité espérée et portefeuille efficient

Si l’espérance de rentabilité d’un titre est supérieure à sa rentabilité exigée, il est possible d’améliorer la performance du portefeuille en augmentant le poids de ce titre dans le portefeuille. Quel poids lui accorder dans le portefeuille ? À mesure que le poids de l’actif i augmente dans le portefeuille, sa corrélation avec celui-ci augmente, ce qui accroît sa rentabilité exigée jusqu’à E [Ri] = ri. En ce point, la pondération du titre i sera optimale. Inversement, si la rentabilité espérée du titre i est inférieure à sa rentabilité exigée, il faut réduire sa pondération, ce qui diminuera sa corrélation avec le portefeuille et donc sa rentabilité exigée ri. Cette réduction du poids de l’actif i doit être poursuivie jusqu’à ce que E [Ri] = ri.

Si l’investisseur ne subit aucune contrainte sur ses transactions, il devrait acheter ou vendre les titres de son portefeuille jusqu’à ce que les espérances de rentabilité de tous les titres soient égales à leurs rentabilités exigées (E [Ri] = ri pour tous les titres i). Aucune nouvelle transaction ne pourra alors améliorer le ratio rentabilité-risque du portefeuille. Ce portefeuille sera alors optimal. Un portefeuille est optimal (ou efficient) si et seulement si la rentabilité espérée de tout titre qui entre dans sa composition est égale à sa rentabilité exigée.

Cela implique l’existence d’une relation entre espérance de rentabilité d’un actif et le bêta de cet actif relativement au portefeuille efficient : 

, avec Reff la rentabilité du portefeuille efficient (le portefeuille ayant le ratio de Sharpe le plus élevé).  βeff  étant la mesure de la sensibilité  de l’actif i aux fluctuations du portefeuille P efficient. Il est déterminé par la formule :

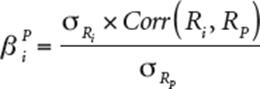
Exemple :

 Pauline a investi dans le fonds Oméga, lequel est composé de diverses classes d’actifs. Son espérance de rentabilité est de 15 % et sa volatilité est de 20 %. Elle détient également des bons du Trésor (sans risque) rémunérés à 3 %. Son courtier lui suggère d’ajouter des parts d’une société civile de placement immobilier (SCPI) à son portefeuille actuel. Ces parts ont une rentabilité espérée de 9 % et une volatilité de 35 %. Leur corrélation avec le fond Oméga est de 10 %. Pauline doit-elle suivre l’avis de son courtier ?

Solution

RI est la rentabilité de la SCPI et RO celle du fonds Oméga. Le bêta de la SCPI relativement au fonds Oméga est :

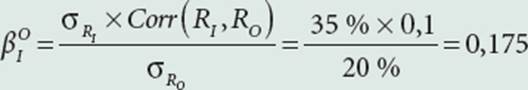
La rentabilité exigée minimale pour que la SCPI constitue une opportunité de placement intéressante pour Pauline est :

À partir du fonds Oméga et  de la SCPI, si l’on suppose que Pauline a investi 100 millions d’euros dans le fonds Oméga, quelle somme supplémentaire doit-elle investir dans la SCPI si elle souhaite constituer le portefeuille efficient combinant ces deux actifs ?

Pour chaque euro investi dans le fonds Oméga, on suppose que Pauline emprunte xI € (elle vend à découvert xI € de bons du Trésor) pour acheter des parts de SCPI. Son portefeuille a donc une rentabilité de :

RP = RO + xI × (RI – rf).

Le tableau suivant  fournit l’espérance de rentabilité et la volatilité du portefeuille de Pauline en fonction de la part xI investie dans la SCPI, grâce aux formules :

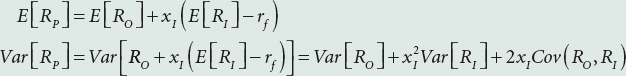
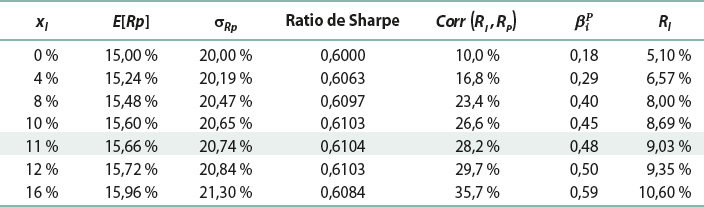
Augmenter la pondération de la SCPI améliore dans un premier temps le ratio de Sharpe du portefeuille de Pauline. Mais à mesure que cette pondération augmente, la corrélation de la rentabilité de la SCPI avec le portefeuille augmente aussi :

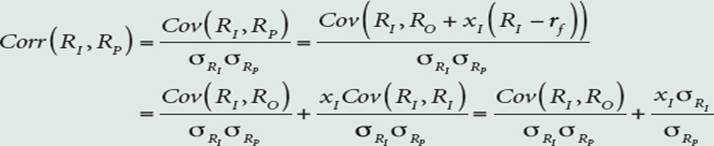
                 Le bêta de la SCPI s’accroît également, ce qui augmente sa rentabilité exigée. Celle-ci est égale à 9 % (l’espérance de rentabilité) lorsque xI = 11 %. Il s’agit de la pondération de la SCPI qui maximise le ratio de Sharpe du portefeuille de Pauline. Le portefeuille efficient constitué de ces deux actifs est ainsi composé de 0,11 € de SCPI pour chaque euro investi en fonds Oméga.

-        Frontière efficiente

Pour choisir un portefeuille, l'investisseur doit théoriquement étudier tous ceux qu'il est possible de constituer à partir de l'ensemble des valeurs existant sur le marché. Une telle démarche, longue et coûteuse, n'est pas nécessaire car ces portefeuilles ne sont pas tous optimaux (efficients). L’ensemble des possibles est représenté dans un espace espérance - écart-type (du rendement).

Exemple 2

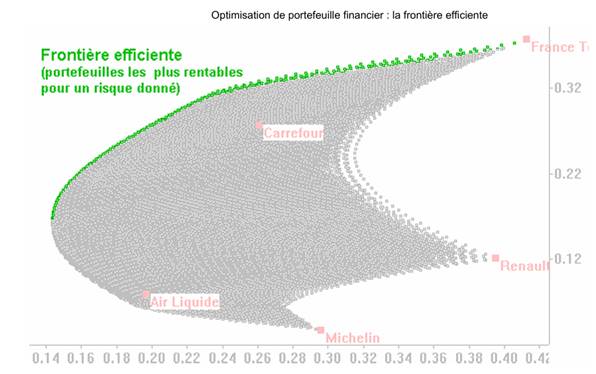
Le graphique ci-dessus montre  le résultat obtenu du  rendement et le risque de quelques milliers de portefeuilles composés de ces cinq valeurs (Air liquide, Carrefour, France Telecom, Michelin et Renault).

En regardant attentivement ce graphique, on peut faire plusieurs constats :

• Le nuage de portefeuilles n'occupe pas tout l'espace. Certaines zones sont totalement inoccupées, ce qui veut dire qu'un grand nombre de combinaisons (risque, rendement) auraient été impossibles à obtenir avec un portefeuille composé de ces valeurs. On peut dire par exemple (et malheureusement sans surprise) qu'il était impossible d'obtenir un rendement élevé avec un faible risque : il n'y a en effet aucun point dans la partie haute à gauche du graphique !

·        Plus généralement, pour un rendement donné, il existe un portefeuille présentant le plus faible risque, et pour un risque donné, il existe un portefeuille présentant le meilleur rendement. Ces portefeuilles 'idéaux' se trouvent tous à la périphérie du nuage et définissent ce que l'on appelle la frontière efficiente (parfois aussi appelée 'frontière efficace').

 

·        L'idéal consiste donc à posséder un portefeuille situé sur la frontière efficiente car c'est la garantie de la maximisation de vos placements.

L'optimisation d'un portefeuille consiste donc à chercher au sein d'un univers de titres donné, les valeurs et les proportions de valeurs permettant de constituer un portefeuille situé sur la frontière efficiente. La puissance du tableur Excel à l’aide de son solveur permet l’optimisation et cette partie du cours vous sera dispensée en EME II dans le cadre du module EXCEL approfondi pour la finance.

 

 

CONCLUSION

Ce cours a doté les participants des outils essentiels pour maîtriser le risque et le rendement. La gestion du risque et du rendement est essentielle pour naviguer avec succès dans les marchés financiers volatils d'aujourd'hui. Une compréhension approfondie des concepts et outils présentés permettra aux auditeurs et futurs investisseurs d'optimiser leurs portefeuilles de manière efficiente.

MERCI